度数分布表には「階級の幅」が重要
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
度数分布表の作り方
について勉強していこうと思います。

そこまで、ちゃんと計算して作る必要はないかもしれません。
しかし、統計学として一つの求め方があるため、紹介させていただきます。
度数分布表

度数布表とは
度数分布表とは、
区間別に現れるデータの個数を表でまとめる
ものです。
度数分布表についてはこちらでも紹介しています
よろしかったらどうぞ
度数分布表を書くとき重要な値に、
階級の幅
があります。
なぜなら、
- 階級の幅が大きすぎては、正確なグラフが描けない階級の幅が狭すぎては、一つ一つのデータが少なすぎて特徴を見つけられない
- 階級の幅が小さすぎては、一つ一つの階級のデータが少なすぎて、特徴が見つけにくい
からです。

実際、ある程度雑に決めても度数分布表はかけますが、
正確な度数分布表を書きたい場合は、こちらの順番で書いてみましょう。
求め方
求める値
度数分布表を作る上で求める値は、
- 最大値・最小値
- 階級の数
- 階級の幅
- 階級値
- 度数
- 相対度数
- 累積度数
があります。
求め方
1、「最大値」・「最小値」を求める
ヒストグラムを作る時に使用するデータの集合の中の一番大きな値 (最大値)・一番小さな値 (最小値)を求めます。

こちらには計算は入りません。
単純に大きい値と小さな値を見つけましょう。
2、「階級の数」を求める
階級の数とは、
表の行の数
です。
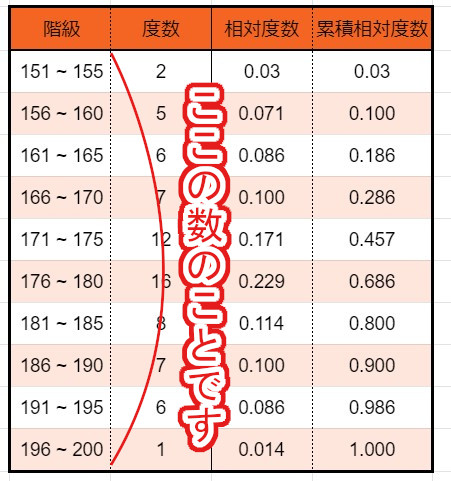
こちらです。
こちらは、スタージェスの公式を使用して求めます。
\(k=\log_{2}n+1\)
\(k\)
階級の幅
\(n\)
データの数
これで、階級の数を求めます。
3、「階級の幅」を求める
階級の幅とは、
一つ一つの階級の範囲
です。
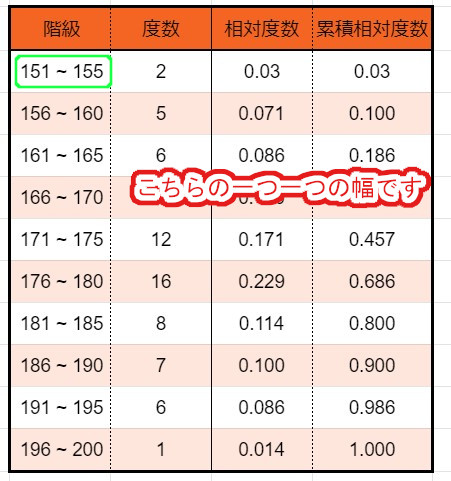
こちらです。
求め方は、
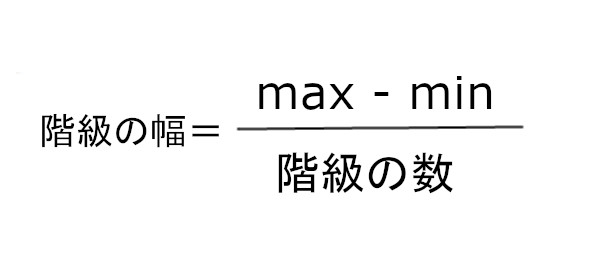
です。
4、「階級値」を求める
階級値とは、
階級の代表値
です。

基本、各階級の中央値がそれにあたります。
求め方は、
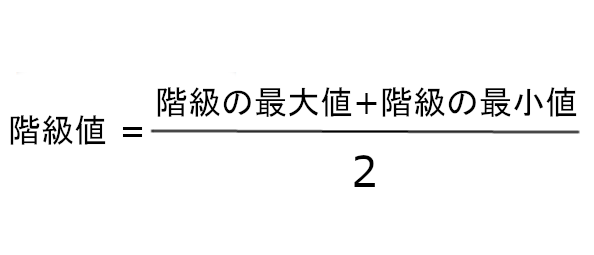
です。
5、「度数」を求める
度数とは、
各階級にあるデータの件数
です。
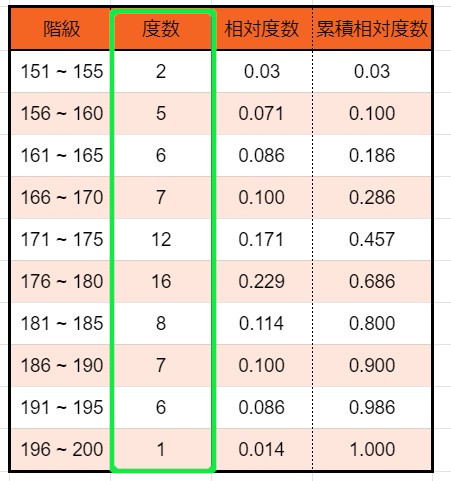
こちらです。

こちらは、各データを数えましょう。
6、「相対度数」を求める
相対度数とは、
各階級の度数の全体からの占める割合
です。
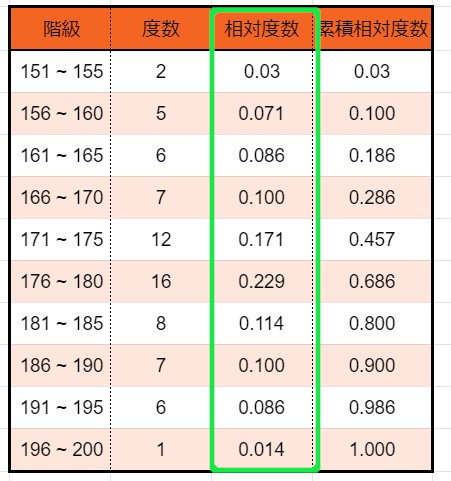
こちらです。
求め方は、
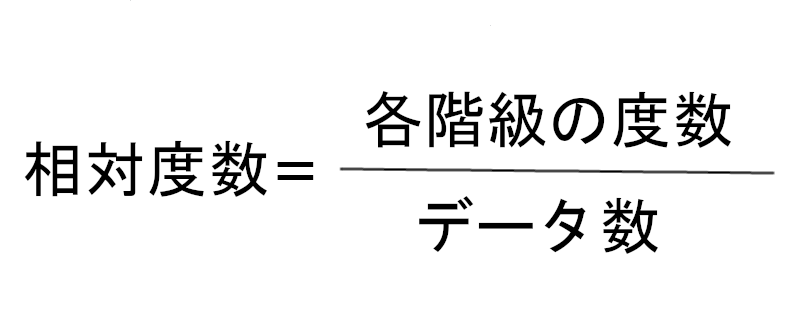
です。
7、「累積相対度数」を求める
累積相対度数とは、
小さい階級から順に相対度数を加えていったもの
です。
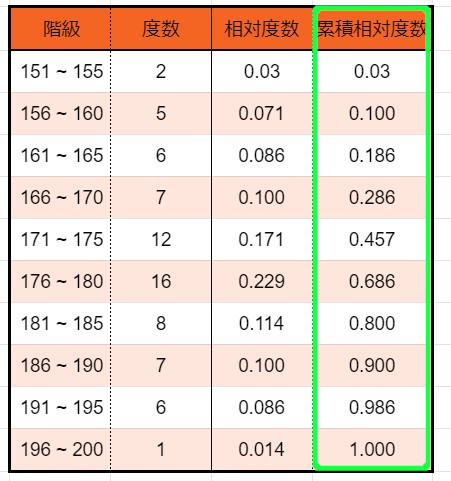
こちらです。

こちらは、そのまま小さい相対係数から足していきましょう。
最後は必ず1になります。
8、表にまとめる
ここまでに求めた値を、表にまとめましょう。
こんな感じで完成です
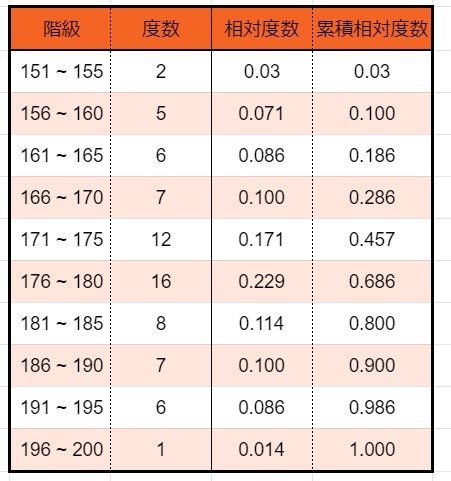
例
度数分布表の作成

1、「最大値」「最小値」を求める
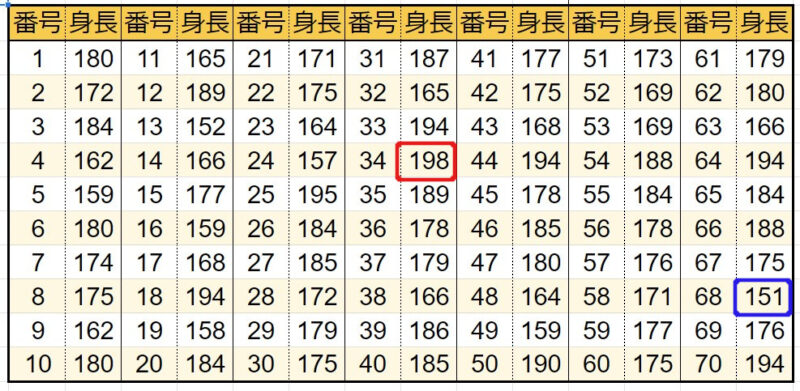
こちらはデータから探しましょう。
最大値は198・最小値は151
2、「階級の数」を求める
求め方は、

です。
データの数が70
式に代入すると,
n = log270 + 1 ≒ 6 + 1 = 7
よって、
階級の数は7
です。

これで、表の行は項目の1行 + 7行です。
3、「階級の幅」を求める
求め方は、
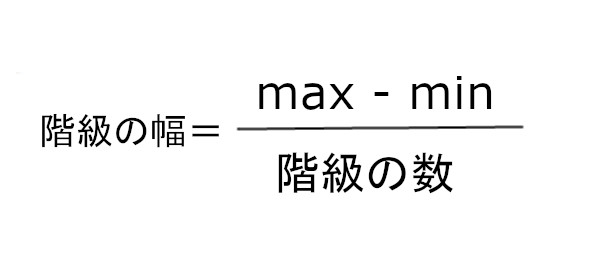
です。
最大値は198・最小値は151でした。
なので、
max – min = 198 – 151 = 47
階級の幅 = 47 / 7 ≒ 7
よって、
階級の幅は7
です。
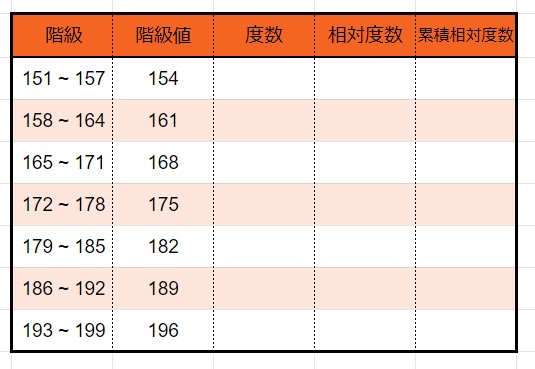
4、「階級値」を求める
各階級の真ん中の値になります。
151 ~ 157 の階級値は154
158 ~ 164 の階級値は161
165 ~ 171 の階級値は168
172 ~ 178 の階級値は175
179 ~ 185 の階級値は182
186 ~ 192 の階級値は189
193 ~ 199 の階級値は196
です。
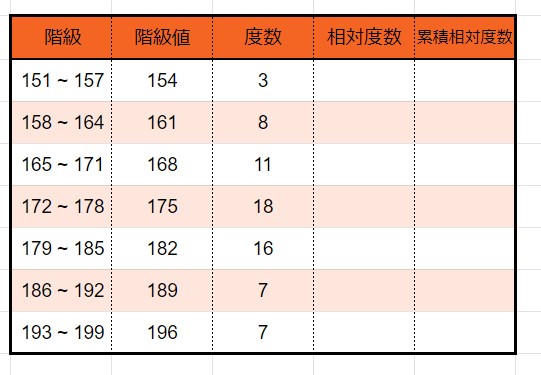
5、「度数」を求める
こちらも数えましょう。
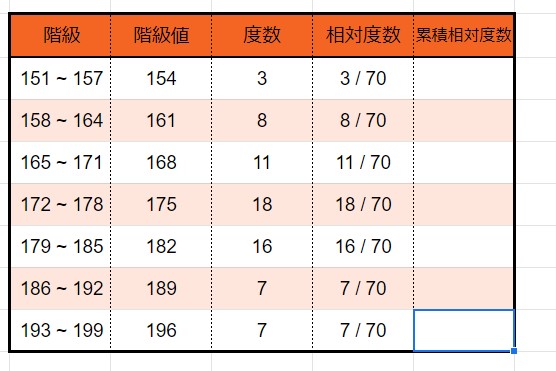
6、「相対度数」を求める
求め方は、

です。
データ数は70
よって、
151 ~ 157 の相対度数は 3 / 70
158 ~ 164 の相対度数は 8 / 70
165 ~ 171 の相対度数は 11 / 70
172 ~ 178 の相対度数は 18 / 70
179 ~ 185 の相対度数は 16 / 70
186 ~ 192 の相対度数は 7 / 70
193 ~ 199 の相対度数は 7 / 70
となります。
7、「累積相対度数」を求める
累積相対度数は足していけば求められます。
よって、
151 ~ 157 の相対度数は 3 / 70
158 ~ 164 の相対度数は 3 / 70 + 8 / 70 = 11 / 70
165 ~ 171 の相対度数は 11 / 70 + 11 / 70 = 22 / 70
172 ~ 178 の相対度数は 22 / 70 + 18 / 70 = 40 / 70
179 ~ 185 の相対度数は 40 / 70 + 16 / 70 = 56 / 70
186 ~ 192 の相対度数は 56 / 70 + 7 / 70 = 63 / 70
193 ~ 199 の相対度数は 63 / 70 + 7 / 70 = 70 / 70
となります。
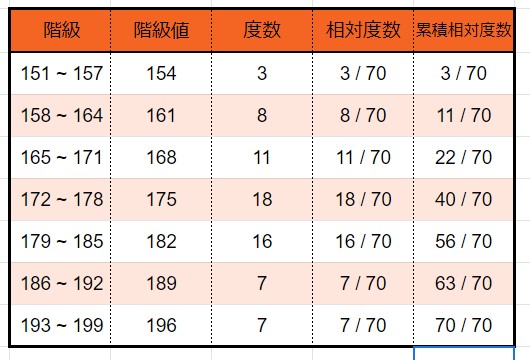

これで度数分布表の出来上がりです。
実際、ここまで計算して度数分布表を作ることはないかもしれません。
まとめ
今回は、「度数分布表の書き方」について紹介させていただきました。
度数分布表を書くときに重要な数値は、
階級の幅
です。
なぜなら、
- 階級の幅が大きすぎては、正確なグラフが描けない
- 階級の幅が狭すぎては、一つ一つのデータが少なすぎて特徴を見つけられない
からです。
なので、スタージェスの公式を使用して、正確な度数分布表の書き方を紹介させていただきました。
実際には、ややこしい計算はその部分のみであとは簡単な計算で出来上がります。
ある程度雑に幅を決めてもそこまで問題ないでしょうが、幅を決める時に困ったらこの書き方をしてみてください。
最後まで読んでいただき、ありがとうございました。




コメント