偏差平方和 = 偏差 + 2乗(平方) + 足す(和)
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
偏差平方和
について勉強していこうと思います。
たくさんのデータから傾向を調べるときに使用するものの一つに平均値があります。
しかし、
- 平均値が同じだから同じような傾向のデータ
- 平均値が全然違うから全く傾向が違うデータ
とは言い切れません。
そんなときに使用する指標の一つが偏差平方和です。
それではよろしくお願いします。
偏差平方和
偏差平方和とは
偏差平方和とは、
各データの散らばり具合の合計
です。
計算式のように書くと、
偏差平方和 = 偏差 + 平方 (2乗) + 和 (足す)
ということです。

つまり、偏差を二乗して物の合計です。
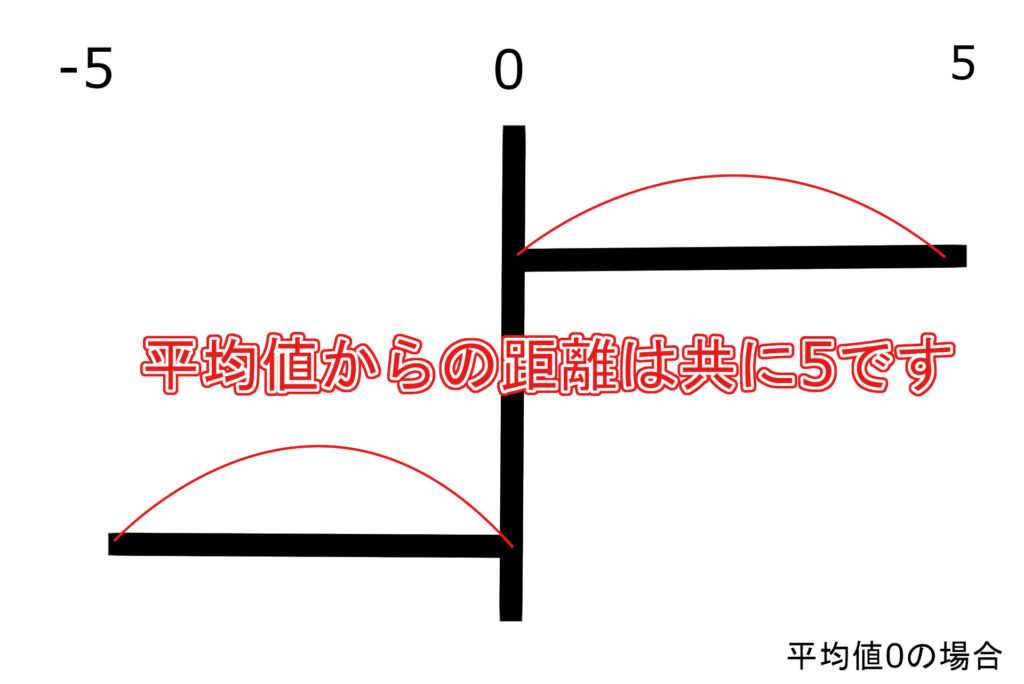
平均値や最頻値が一緒でもデータが全く同じというわけでありません。
そのため、平均からの各データの距離 (偏差) を見て比較する必要があります。
偏差平方和は、その距離の合計です。
偏差
偏差とは、
平均方の各データの散らばり具合
です。
偏差ついてはこちらでも紹介しています
よろしかったらどうぞ
平方
数学では平方とは、
2乗する
ことを意味します。
先ほど説明したように、偏差がマイナスになってしまう値をプラスにするために、2乗しましょう。
和
和は、
足す
という意味です。
合計を出すため、全ての値を足します。
求め方
求め方は、
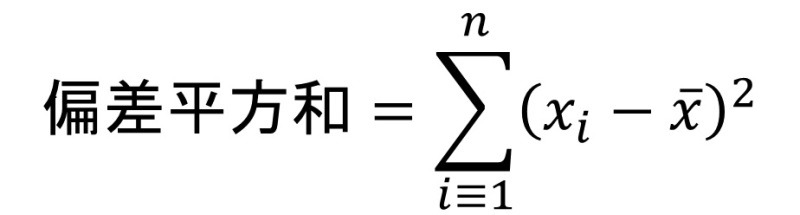
です。
これを崩して書くと、
偏差平方和 = (データ1の偏差)2 + (データ2の偏差)2 + ・・・ + (データnの偏差)2
となり、偏差 = 各データ – 平均値なので、
偏差平方和 = (データ1 – 平均値)2 + (データ2 – 平均値)2 + ・・・ + (データn – 平均値)2
となります。
特徴
平均値などの違いではみられない違いがわかることもある
先ほど話したように、平均値・中央値・最頻値がどれも同じでも、全く違うヒストグラムになる事がよくあります。
平均からの散らばりから違いを考えてみましょう。
偏差平方和から他の値を求められる
偏差平方和も統計学で使われる値の一つです。
しかし、偏差平方和のみで傾向を見るのではなく、
標準偏差・分散
などがあります。

実際の比較には「標準偏差」がよく使われますが、いきなり「標準偏差」の説明では、真ん中を飛ばしすぎているため、理解しづらいです。
平均値 → 偏差 → 偏差平方和 → 分散 → 標準偏差
という流れで分散が解けるので、順番に理解していきましょう。
注意点

偏差平方和の大きさだけで判断してはいけない
偏差平方和とは、距離の合計です。
つまり、データが多いほど偏差平方和も大きくなります。
なので、偏差平方和の大きさで二つ以上の集合を比較する場合、
必ずデータの数
に注目しましょう。
データが5個の偏差平方和より、100個の偏差平方和の方が大きくても何も不思議ではありません。
逆に、5個の偏差平方和の方が大きかったら、
そちらの平均から大きく離れているデータが1つ以上存在する or 100個のうちほとんどの値が平均からあまり離れていない
ことを意味します。

このように、何も得られないわけではありませんが、データの数にも注目していないと勘違いしてしまう恐れはあります。
気をつけましょう。
まとめ
今回は、偏差平方和について、紹介させていただきました。
この値は、平均からの距離の合計です。
偏差平方和は、
- 偏差:各データの平均からの距離
- 平方:2乗
- 和 :合計
のため、名前通りのことを順番に行って求めます。
平均値・中央値・最頻値ではわからない傾向を掴むのに重要になる値です。
また、特徴にも書きましたが、この値から
標準偏差・分散
などの統計学でもっと使われる値を求めます。
そちらを理解するためにも重要な値になります。
求め方や特徴を理解し、データの一つとして求めてみましょう。
また、注意すべき点は、偏差平方和の大きさで比較する場合は、
必ずデータの数にも注目すべき
だということです。
最後まで読んでいただき、ありがとうございました。




コメント