標準偏差 = √分散
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
標準偏差
について勉強していこうと思います。
たくさんのデータから傾向を調べるときに使用するものの一つに平均値があります。
しかし、
- 平均値が同じだから同じような傾向のデータ
- 平均値が全然違うから全く傾向が違うデータ
とは言い切れません。
そんなときに使用する指標の一つが標準偏差です。
それではよろしくお願いします。
標準偏差
標準偏差とは
標準偏差とは、
データのバラツキの平均
です。

説明としては分散と同じです。
計算式のように書くと、
標準偏差 = √分散
となります。
標準偏差は、
平均値 → 偏差平方和 → 分散 → 標準偏差
の順番で求めることができます。
平均値 → 偏差平方和の時に、
距離の合計を出すために平方(2乗)
をしています。
そのため、分散の時点で求めたバラツキ具合の平均とは、
二乗した値の平均
になります。
そのため、√を使い、実際の距離の平均を求めたものが、標準偏差となります。
つまりこの標準偏差が、実際の平均値の距離の平均になります。
バラツキの平均が出せるため、
- 「標準偏差」が大きいほど、各データがバラけている
- 「標準偏差」が小さいほど、各データがバラけておらず、平均付近のデータが多い
ことがわかります。
求め方
求め方は、
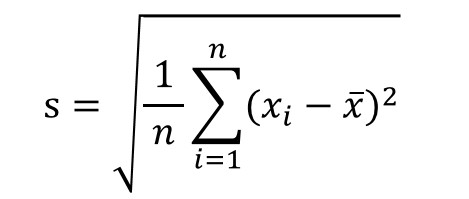
です。
この![]() が標準偏差です。
が標準偏差です。
特徴
平均値などの違いではみられない違いがわかることもある
分散などと同じように、平均値・中央値・最頻値がどれも同じでも、全く違うヒストグラムになる事がよくあります。
平均からのバラツキから違いを考えてみましょう。
データの傾向が掴みやすくなる
標準偏差を求めることで、
以降のデータが平均からどのくらい離れた値の可能性が高いか
が予測できます。
- 標準偏差が大きいほど、平均から離れた値が出る可能性が高い
- 標準偏差が小さいほど、平均あたりの可能性が高い
という予測が立てられます。
しかし、あくまで統計であり予測です。
その範囲以外の値が出ることも当然あります。
また、データが増えるうちに標準偏差も変化していくこともあります。
しかし、かなりのデータで計算した場合は大きく変化はなくなります。

途中の計算でデータ数が分母のため、
一つの値が与える影響が少ないですからね。
例
二つのデータの比較

1、左のデータから「標準偏差」を求める

ヒストグラムにすると
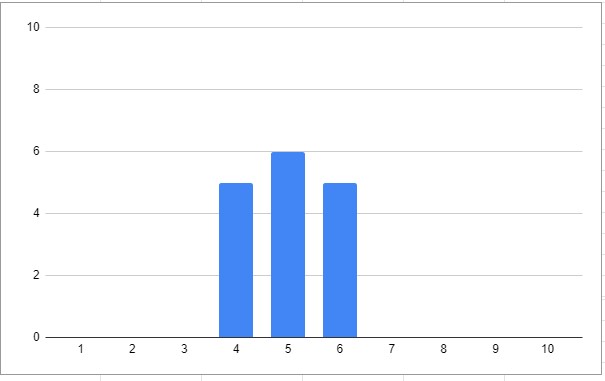
です。
1.1、「データの数」・「値の合計」を算出
データの数は
5 + 6 + 5 = 16
です。
値の合計は
4×5 + 5×6 + 6×5 = 20 + 30 + 30 = 80
です。
1.2、「平均値」を算出
平均値は、値の合計 / データの数 のため、
80 / 16 = 5
です。
1.3、「偏差」を算出
偏差は、各データの平均との差のため、
4 – 5 = -1 で-1が5件
5 – 5 = 0で0が6件
6 – 5 = 1 で1が5件
です。
1.4、「偏差平方和」を算出
偏差平方和は、各偏差の2乗の合計のため、
{(-1)2 × 5 } + { 02 × 6 } + { 12 × 5 }
= 5 + 0 + 5
= 10
です。
1.5、「分散」を算出
分散は、偏差平方和 / データの数のため、
10 / 16 = 0.625
です。
1.6、「標準偏差」を算出
標準偏差は、√分散のため、
√0.625 ≒ 0.79
です。
つまり、こちらのデータは、平均値から平均で0.79上下にバラけているということになります。
2、右のデータの「標準偏差」を求める

ヒストグラムにすると、
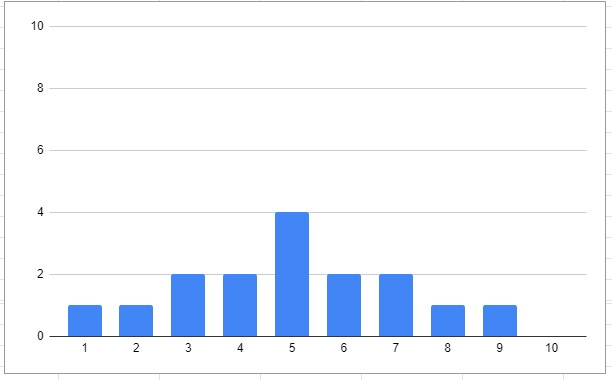
です。
2.1、「データの数」・「値の合計」を算出
データの数は
1 + 1 + 2 + 2 + 4 + 2 + 2 +1 + 1 = 16
です。
値の合計は
1×1 + 2×1 + 3×2 + 4×2 + 5×4 + 6×2 + 7×2 + 8×1 + 9×1
= 1 + 2 + 6 + 8 + 20 + 12 + 14 + 8 + 9 = 80
です。
2.2、「平均値」を算出
平均値は、値の合計 / データの数 のため、
80 / 16 = 5
です。

平均値は、二つとも同じですね。
2.3、「偏差」を算出
偏差は、各データの平均との差のため、
1 – 5 = –4が1件
2 – 5 = -3が1件
3 – 5 = -2が2件
4 – 5 = -1が2件
5 – 5 = 0が4件
6 – 5 = 1が2件
7 – 5 = 2が2件
8 – 5 = 3が1件
9 – 5 = 4が1件
です。
2.4、「偏差平方和」を算出
偏差平方和は、各偏差の2乗の合計のため、
{ (-4)2 × 1 } + { (-3)2 × 1 } + { (-2)2 × 2 } + { (-1)2 × 2 } + { 02 × 4 } + { 12 × 2 } + { 22 × 2 } + { 32 × 1 } + { 42 × 1 }
= 16 + 9 + 8 + 2 + 0 + 2 + 8 + 9 + 16
= 70
です。
2.5、「分散」を算出
分散は、偏差平方和 / データの数のため、
70 / 16 = 4.375
です。
2.6、「標準偏差」を算出
標準偏差は、√分散のため、
√4.375 ≒ 2.09
です。
つまり、こちらのデータは、平均値から平均で2.09上下にバラけているということになります。
3、二つの「標準偏差」を比較
先程の二つのデータの「標準偏差」を比較をします。
左の標準偏差
0.79
右の標準偏差
2.09
左のデータの方が平均からのバラツキ(標準偏差)が少なく、以降データを取っても、右のデータよりも平均値近くになる可能性が高い。
右のデータの方が平均からのバラツキ(標準偏差)が大きく、以降データを取っても、左のデータよりも平均値から離れたデータになる可能性が高い。

データの数が大きいほどその可能性は高くなると考えられます。
今回のデータは一桁の数字で計算したためわかりにくいかもしれません。
全てのデータを1万円かけて別々のお店A・Bの売り上げで考えてみましょう。
| A | B | |
| 日数 | 16日 | 16日 |
| 総売上 | 80万円 | 80万円 |
| 平均値 | 5万円 | 5万円 |
| 偏差平方和 | 10万 | 70万 |
| 分散 | 0.625万 | 4.375万 |
| 標準偏差 | 0.79万円 | 2.09万円 |
このようになります。

「偏差平方和」「分散」は2乗した値だということを忘れないようにしましょう。
A・Bどちらも16日間の平均売り上げは5万円です。
しかし、バラツキの平均(標準偏差)は、
A:0.79万円・B:2.09万円
です。
A店よりもB店の方が、売上の上下が激しいと考えられます。
まとめ
今回は、標準偏差について紹介させていただきました。
この値は、散らばりの平均です。
求め方は、
標準偏差 = √分散
です。
分散を求めるまでに、
値を2乗
しています。
なので、√を使用して2乗外しましょう。
これにより、実際の平均値からのバラツキ具合がわかります。
標準偏差を求めることで、
そのデータの傾向
が掴みやすくなります。
最後まで読んでいただきありがとうございました。



コメント