極端に離れた値
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
は、いきましょう!
統計学
今回は、
はずれ値
について勉強していこうと思います。
はずれ値
はずれ値とは平均から極端に離れた値
はずれ値とは、
平均値より極端に大きいまたは極端に小さい値
です。

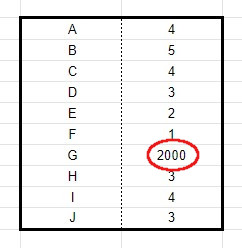
他のデータが「4・5・6」の中で、
一つのデータだけ「1000」などがあった場合などです。
はずれ値を入れて計算すると結果は大きく変わることもある
例えば

この値をどう思いますか?
他の値と比べて非常に大きく離れて見えます。
この値を入れた場合と入れない場合の平均値を求めてみましょう。
入れる場合
(4+5+4+3+2+1+2000+3+4+3) / 10
= 2029 / 10 = 202.9
入れない場合
(4+5+4+3+2+1+3+4+3) / 9
= 29 / 9 ≒ 3.2
このように、
平均値が大きく変わる
ことになります。

このデータ群の平均値が202.9は大きすぎると思いますよね。
そして、
標準偏差・変動係数・相関係数
などは平均値を使って求めます。
つまり、
平均値が大きく変わってしまっては、他の値も大きく変わってしまう
こともあります。
どんな時にはずれ値が出現する?
では、どのような時にはずれ値は出現するのでしょうか?

平均値を大きく変えてしまうほどの値です。
そう滅多に出現する値ではないですよね。
- お店などで1日だけ大量の予約は入った
- 台風などによりお客さまがその日だけ全然来なかった
- 入力ミス
などがあります。

入力ミスは実際には「異常値」となります。
しかし、入力ミスと解るのははずれ値とわかった後のこともあります。
はずれ値かどうかの判断
問題は、その値がはずれ値がどうかの判断です。

表やグラフを見ただけで判断するのは、理由としては弱いですよね。
判断の仕方としては、
箱ひげ図
があります。
箱ひげ図
はずれ値を判断する方法の一つに、
箱ひげ図の作成
があります。
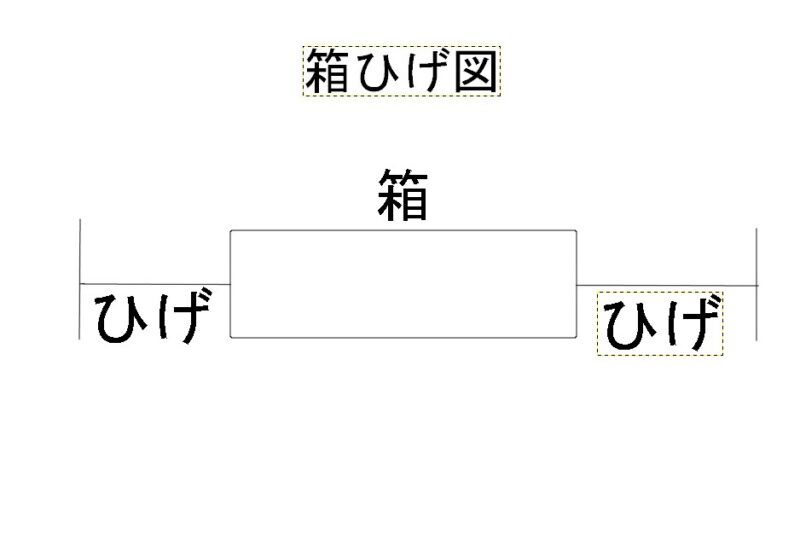
このような図のことです。
箱ひげ図は、
- 最小値
- 最大値
- 中央値
- 第一四分位数
- 第三四分位数
の5つ値から求められます。
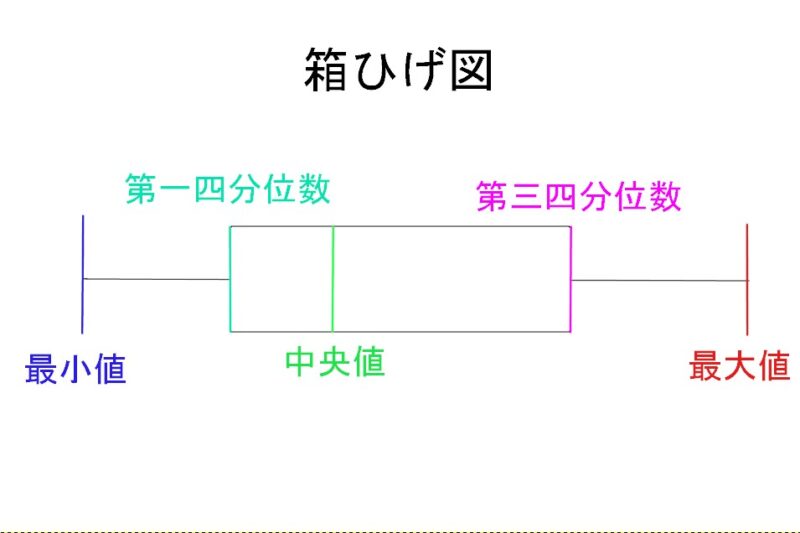
この図で、
箱の長さ × 1.5 より長いひげははずれ値となる
のです。
つまり、
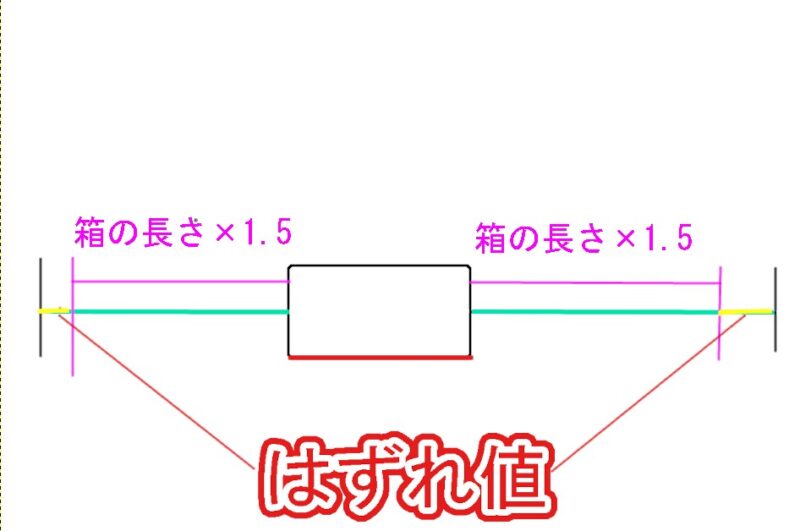
と言うことです。
また、箱ひげ図に関しては、次回もう少し細かく紹介させていただきます。
注意点
もう一度データの確認をしましょう
はずれ値は、極端に離れた値です。
しかし、これは入力ミスの可能性もあり得ます。

入力をミスしていないかもう一度確認してみましょう。
はずれ値だからといって全て外していいわけではない
はずれ値も、入力ミスでないのなら明らかに示されたデータの一つです。
そして、はずれ値は平均値により変化します。
つまり、データ数が増えていくにつれて、
その値は外れ値ではなくなることもある
ということです。

あくまで、現在の計算上はずれ値と判断されただけということです。
ある程度データが集まったらもう一度計算してみましょう。
まとめ
今回は、
はずれ値
について紹介させていただきました。
はずれ値とは、
平均値から極端に離れた値
のことです。
はずれ値かどうかの判断は、
表や散布図
で自分で判断することが多いです。
しかし、自己判断のみでは信頼性を落とす結果になってしまうこともあり得ます。
その時は、
箱ひげ図
で求めましょう。
注意点としては、
- 入力ミスの可能性がある
- データが増えることで外れ値ではなくなることもある
ということです。
最後まで読んでいただきありがとうございました。



コメント