はずれ値を見つけるための図
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
箱ひげ図
について勉強していこうと思います。
箱ひげ図
箱ひげ図とは
箱ひげ図とは、
データのバラツキをわかりやすく表現する図
です。
このような図です。
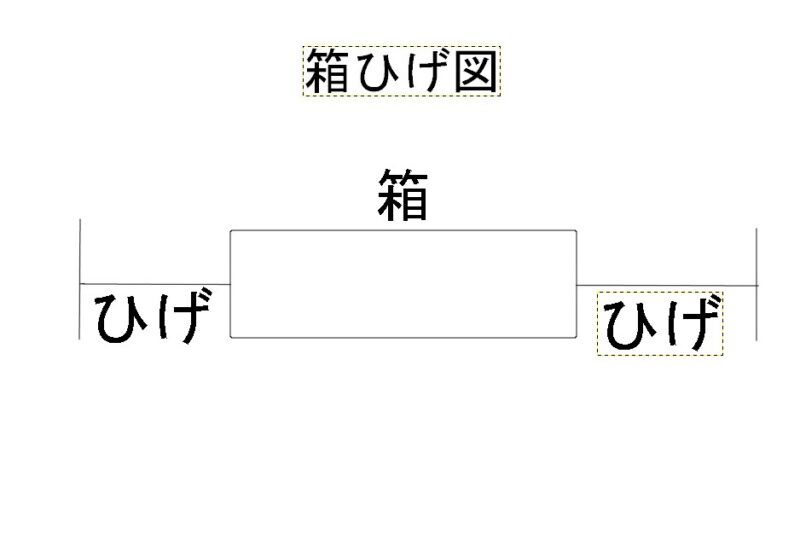
図のように、
四角になっている部分を箱・線の部分をひげ
と呼びます。
箱とひげ
合わせて箱ひげ図です。
書き方
使用する値
箱ひげ図には、主に
最小値
第1四分位値
中央値
第3四分位値
最大値
の5つの値を使用します。
この5つの値を使用して分析することを
5数要約
と言います。
1、最小値・最大値を見つける
この二つは、データの一番小さい値と一番大きい値になります。
この二つに計算はいりません。
データを並べて最小値と最大値を見つけましょう。
2、中央値を見つける
中央値とは、
データ数の真ん中の値
です。
数値の真ん中ではなく、個数での真ん中です。
データの真ん中の値を見つけましょう。
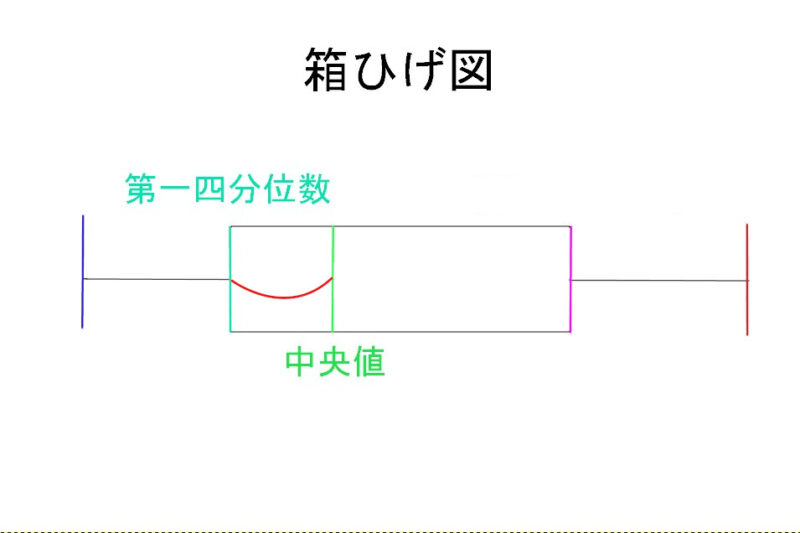
3、第1四分位値と第3四分位値を見つける
第1四分位値とは、
最小値から中央値の範囲の中央値
です。
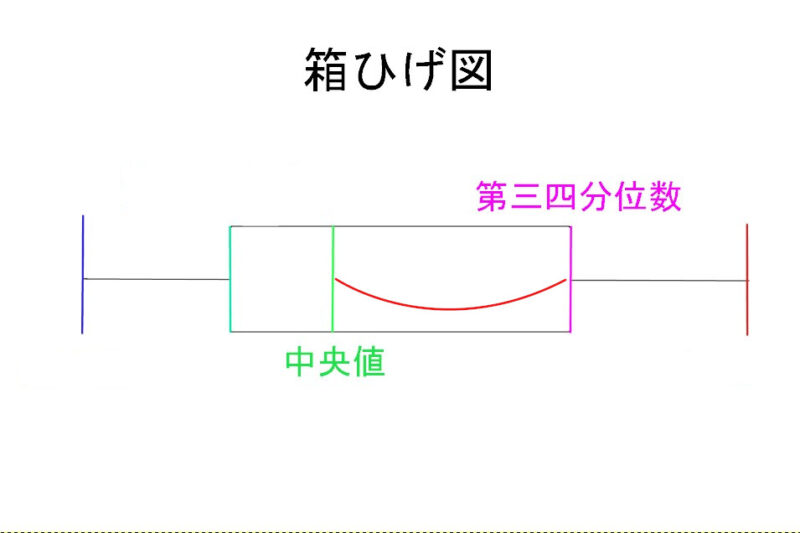
また、第3四分位値とは、
中央値から最大値の範囲の中央値
です。
こちらも求めるのはあくまで中央値です。
よって、難しい計算はいりません。
4、合わせてつなげる
5つの値を見つけられたら、あとは繋げるのみです。
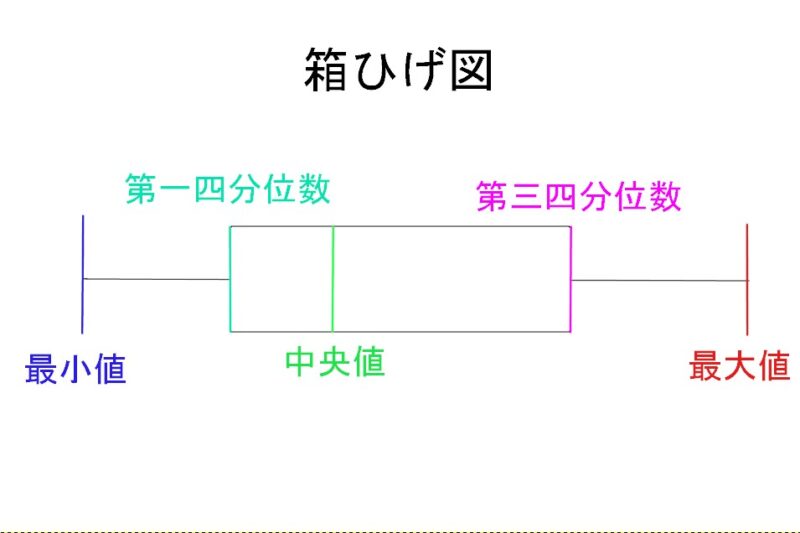
見かた
箱ひげ図は25%づつに分けた図
先ほど、箱ひげ図の書き方を紹介しました。
気づいた方もいらっしゃると思いますが、
箱ひげ図は最小値・最大値と3つの中央値からできた図
になります。
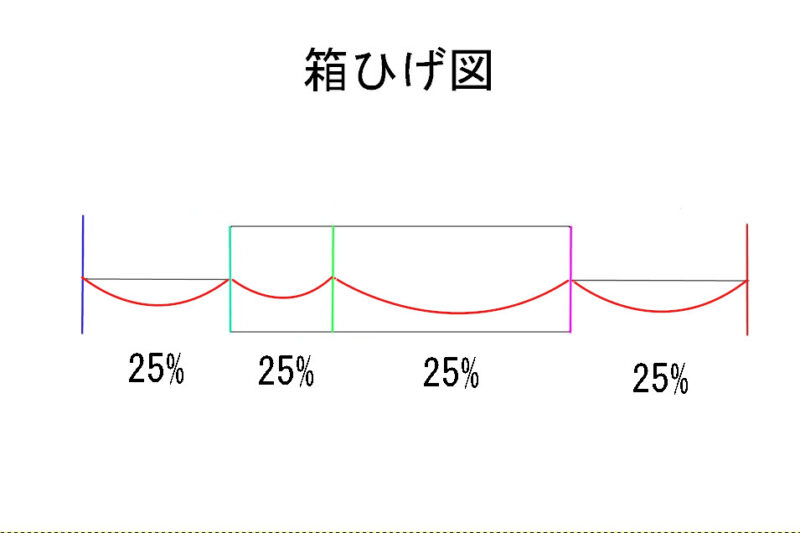
つまり、
- 最小値から第1四分位値までで25%
- 第1四分位値から中央値までで25%
- 中央値から第3四分位値までで25%
- 第3四分位値から最大値までで25%
のデータ数が入っているということです。
用途
箱ひげ図の用途は、主に
- データのバラツキ具合を見る
- 複数のデータのバラツキ具合の比較
- はずれ値を見つける
の2つです。
データのバラツキを見る
箱ひげ図では、
データのバラツキを見る
ことができます。
主に、箱やひげの長さで比較をしましょう。
先程の箱ひげ図を見てみましょう。
この図では、
第1四分位数から中央値よりも中央値から第3四分位数の方が長く
見えます。
第1から中央
中央から第3
よって、
第一四分位数から中央値までの方が狭い範囲にデータ数が集まっている
といえます。
複数のデータのバラツキ具合の比較
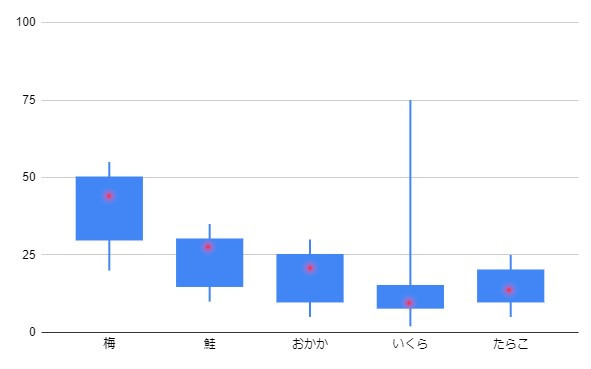
箱ひげ図では、
複数の図を並べることでバラツキ具合の比較
をすることができます。
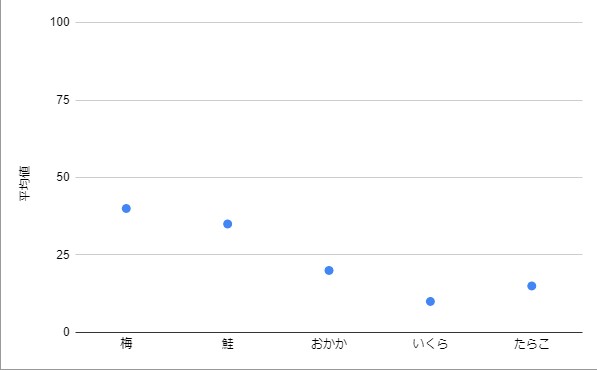
よく、複数のデータの比較には、平均値を使用します。
しかし、平均値だけでは見つけられないこともあります。
そんな時に、箱ひげ図で比較してみましょう。
こちらは、5つのおにぎりの売上個数の平均値を表しています。
平均をみたら、いくらが一番売れていないように見えますね。
こちらを、箱ひげ図で見ると
となったとします。
どうでしょうか?
平均値のみでは、一番少なかった「いくら」が実は一番最大値が多かったのです。
つまり、
平均にすると一番少ないけれども、一番売れることもある
ということがわかります。
はずれ値を見つける
箱ひげ図で、
はずれ値を見つける
ことができます。
はずれ値とは、
平均値より極端に離れた値
のことです。
はずれ値は、
箱の長さ × 1.5 より長いひげに値する値
です。
つまり、
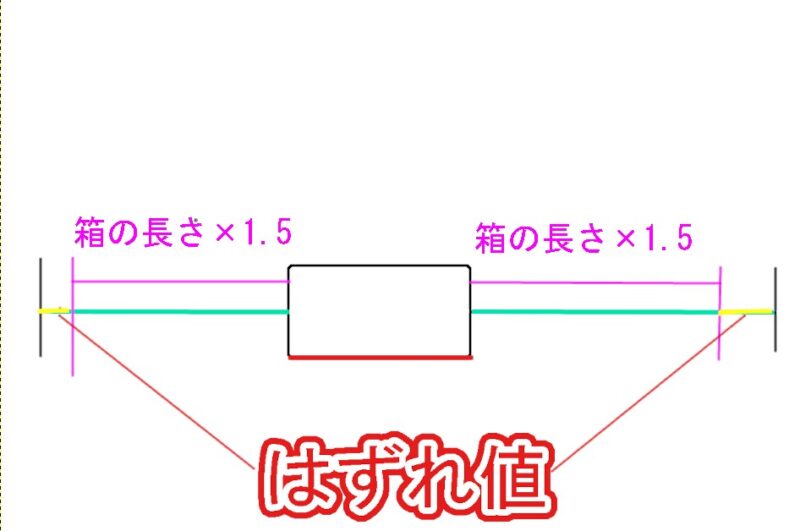
と言うことです。
はずれ値についてはこちらでも紹介しています。
よろしかったらどうぞ
注意点
もう一度データの確認をしましょう
はずれ値は、極端に離れた値です。
しかし、これは入力ミスの可能性もあり得ます。
入力をミスしていないかもう一度確認してみましょう。
はずれ値だからといって全て外していいわけではない
はずれ値も、入力ミスでないのなら明らかに示されたデータの一つです。
そして、はずれ値は平均値により変化します。
つまり、データ数が増えていくにつれて、
その値は外れ値ではなくなることもある
ということです。
あくまで、現在の計算上はずれ値と判断されただけということです。
ある程度データが集まったらもう一度計算してみましょう。
まとめ
今回は、「箱ひげ図」について紹介させていただきました。
箱ひげ図とは、
データのバラツキをわかりやすく表現する図
です。
箱ひげ図は、
- 最小値
- 第1四分位数
- 中央値
- 第3四分位数
- 最大値
の5つの値で作ります。
用途としては、
- データのバラツキ具合を見る
- 複数のデータのバラツキ具合の比較
- はずれ値を見つける
時に使用します。
注意点は、
- 入力ミスの可能性がある
- データが増えることで外れ値ではなくなることもある
です。
最後まで読んでいただき、ありがとうございました。
コメント