相対度数から格差を見つける
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
ローレンツ曲線
について紹介します。
よく、
会社全体が支払う給料の80%は上位5%に支払われる
(数字は架空のものです)
など聞いたことありませんか?

この数字でいくと、
残りの20%を95%の人で分けていることになりますよね。
このようなものを
格差
と言います。

完全に均等とはいかないにしても、
広すぎる格差は不均等ですよね。
今回は、そんな格差を曲線で表した
ローレンツ曲線
についての説明です。
それでは、よろしくお願いします。
ローレンツ曲線とは
ローレンツ曲線とは
まずローレンツ曲線を見てみましょう。
ローレンツ曲線とは、
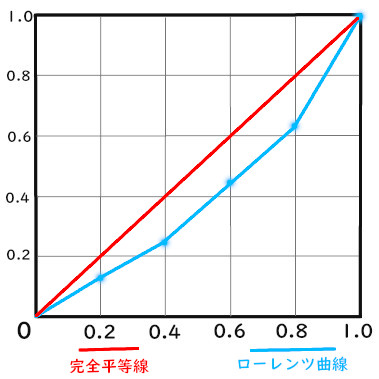
このような曲線のことです。

曲がっている線のことをローレンツ曲線と言います。
こちらは、大きく二つの線、
があります。
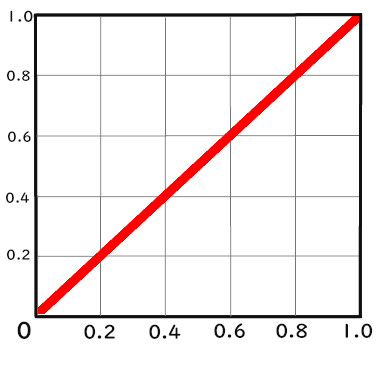
完全平等線
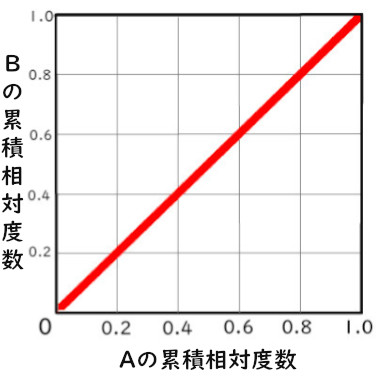
完全平等線とは、
全く格差のない時の線
です。

全体を綺麗に四等分されたときの
ローレンツ曲線はこの線と同じになります。
実際には、
ローレンツ曲線が完全平等線とどのくらい離れているかを見る
ために使用します。
ローレンツ曲線
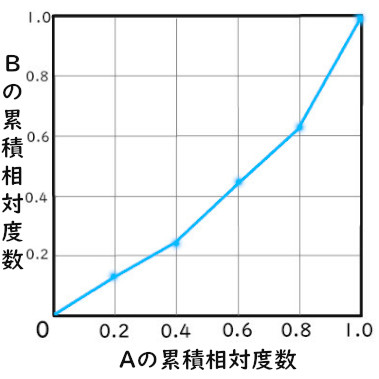
このように、
左辺・下辺ともに累積相対度数の折れ線グラフ
になります。

こちらでは5等分していますが、
4等分・10等分などでも問題ありません。
完全平等線との乖離具合で格差がどのくらいあるかを見ます。

ちなみに全く格差がない場合、
ローレンツ曲線は完全平等線と同じになります。
必ず
最初の点
0
最後の点
1
になります。
また、ローレンツ曲線のいい点は、
元のデータの単位によらない
ことです。

両辺とも累積相対度数のため、
二つの曲線を比較するとき、そのまま一緒のグラフに書けます。
使い方
ローレンツ曲線の使い方としては、主に
- 両辺の値から各部分の割合を見つける
- 二つを見比べて乖離具合を比較する
- ジニ係数を求める
などがあります。
両辺の値から各部分の割合を見つける
先ほどのローレンツ曲線を見ると、
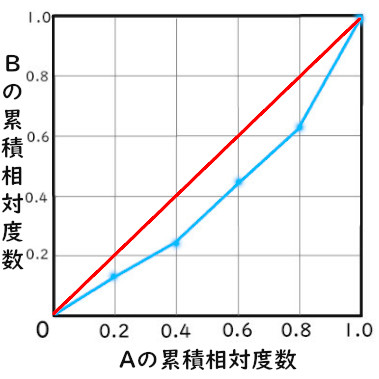
- Bが半分の時のAの割合が約7割ある
- Aの上位2割がBの約4割を占めている
などがわかります。
Bが半分の時のAの割合が約7割ある
グラフの
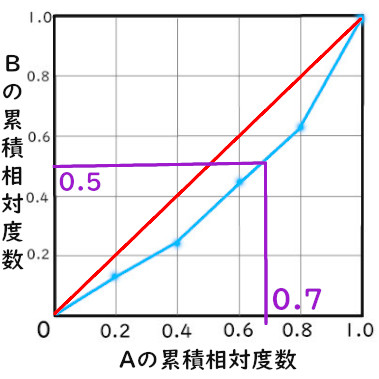
この部分を見ることでわかります。
Aの上位2割がBの約4割を占めている
グラフの
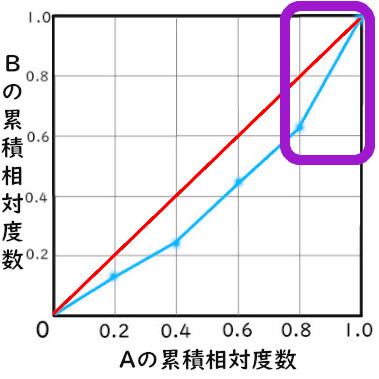
この部分を見ることでわかります。
つまり、
残りの6割を8割が占める
ということです。

これが格差ですね。
二つを見比べて乖離具合を比較する
例えば、
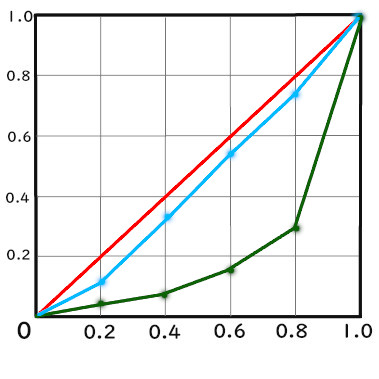
があるとします。

先ほども書きましたが、単位によらないため、
このようにまとめて曲線を書けます。
この2本の曲線を見比べると、
- 緑より青の方が格差が少ない
- 青の0.4までの割合を緑は0.8が占めている
などを見つけることができます。
緑より青の方が格差が少ない
グラフの
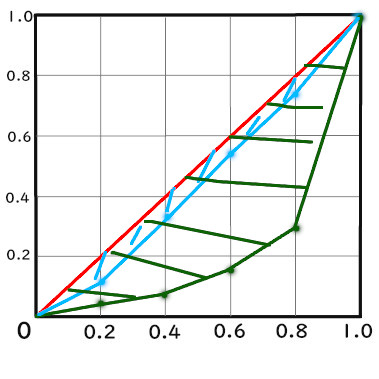
この部分を見ることでわかります。
面積が大きいほど、
格差が大きい
ということになります。
青の0.4までの割合を緑は0.8が占めている
グラフの
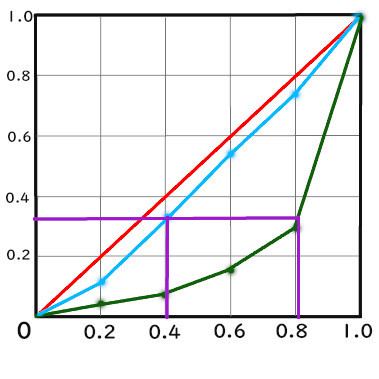
この部分を見ることでわかります。
つまり、
残りの6割を8割が占める
ということです。

これが格差ですね。
ジニ係数を求める
ローレンツ曲線から時に係数を求めることができます。
ジニ係数とは、
格差を数値で表した係数
です。

ローレンツ曲線の面積から求めます。
ジニ係数ついては後日紹介させていただきます
ローレンツ曲線の作り方
ローレンツ曲線の作り方は、
①データを小さい順に並べる
↓
②各累積相対度数と求める
↓
③折れ線グラフを作る
です。
例
横軸
人の累積相対度数
縦軸
身長の累積相対度数
として考えましょう。
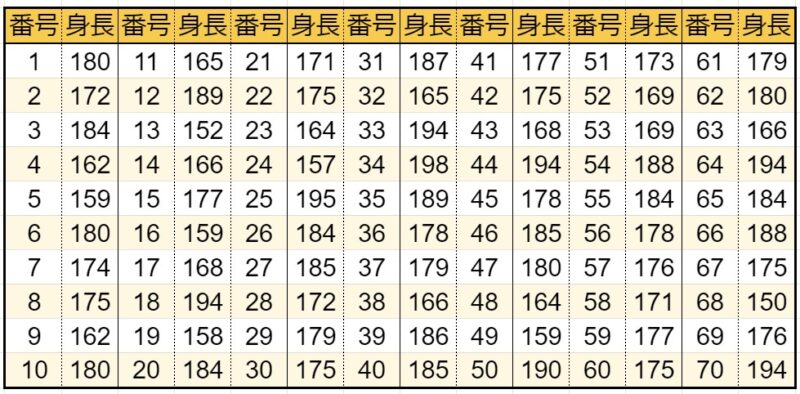
1、データを小さい順に並べる
まずは、データを小さい順に並べましょう。
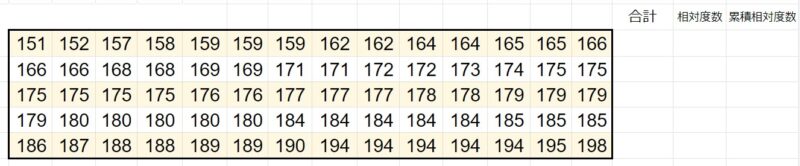
2、各累積相対度数を求める
では、各累積相対度数を求めましょう。
2.1、横軸の累積相対度数
今回、横軸は人にしました。
そのため、
人の累積相対度数
を求めましょう。
2.1.1、合計を求める
人の合計は、
70人
です。
2.1.2、分けたい分にデータを分ける
今回は、5等分します。

つまり、20%づつですね。
よって、
1~14人目
15~28人目
29~42人目
43~56人目
57~70人目
となります。
2.1.3、累積相対度数を求める
人の場合、どの人も1人であり差がないため、そのまま5等分で問題ありません。
よって、
1~14人目
0.2
15~28人目
0.4
29~42人目
0.6
43~56人目
0.8
57~70人目
1.0
となります。
2.2、縦軸の累積相対度数
縦軸は身長にしました。
そのため、身長の累積相対度数を求めます。
2.2.1、合計を求める

身長の合計は、
12341
です。
2.2.2、分けたい分にデータを分ける
今回は、5等分します。

つまり、20%づつですね。


今回は、元々5等分に分けていたため、
変化はありません。
2.2.3、各合計を求める
各合計を求めましょう。
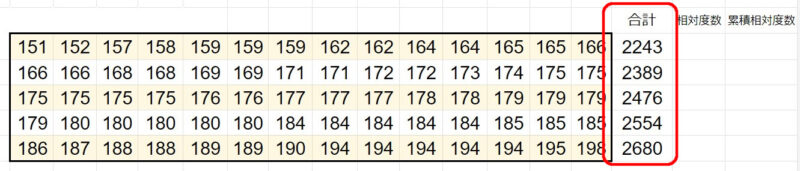
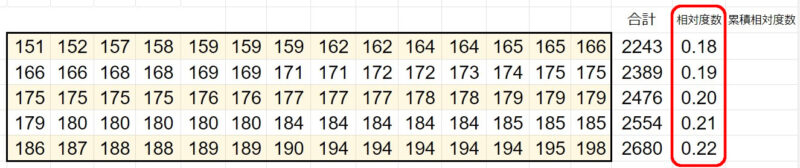
2.2.4、相対度数を求める
次に、各相対度数を求めましょう。
2243 / 12341
= 0.18
2389 / 12341
= 0.19
2476 / 12341
= 0.20
2554 / 12341
= 0.21
2680 / 12341
= 0.22
となります。
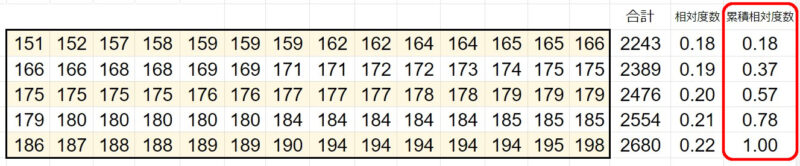
2.2.5、累積相対度数を求める
次に、各累積相対度数を求めましょう。
よって、
1~14人目
0 + 0.18
= 0.18
15~28人目
0.18 + 0.19
= 0.37
29~42人目
0.37 + 0.20
= 0.57
43~56人目
0.57 + 0.21
= 0.78
57~70人目
0.78 + 0.22
= 1.00
となります。
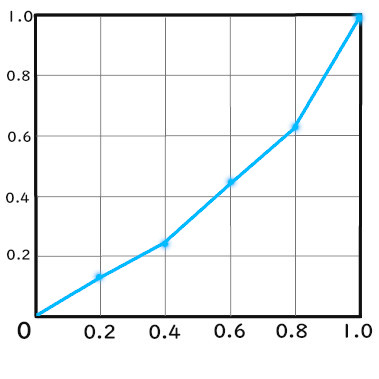
3、折れ線グラフを作る
今求めた各累積相対度数から折れ線グラフを作りましょう。
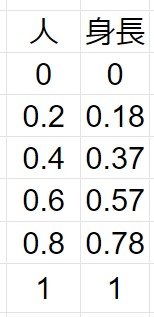

二つの累積相対度数から折れ線グラフを作りましょう。
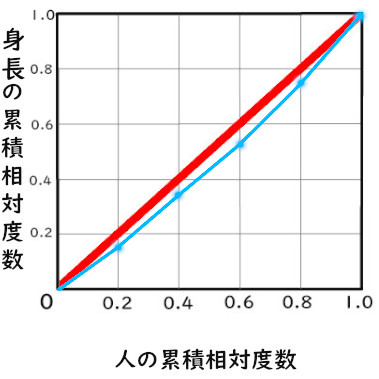

これでローレンツ曲線ができました。
今回は、それほど乖離のない結果になりました。
まとめ
今回、
ローレンツ曲線
について紹介させていただきました。
ローレンツ曲線とは、
データの乖離具合を調べる曲線
です。
ローレンツ曲線を求めるために必要なのは、
各累積相対度数
です。
ローレンツ曲線を求めることで、
- 両辺の値から各部分の割合を見つける
- 二つの曲線を見比べて乖離具合を比較する
- ジニ係数を求める
などができます。

ジニ係数を求めるときによく使用します。
乖離具合を調べることで、
全体の中の格差を知る
ことができます。

4等分して、
- 下位25%にどのくらいあるのか
- 真ん中の50%にどのくらい集まっているのか
などを知ることができます。
最後まで読んでいただき、ありがとうございました。



コメント