ローレンツ曲線から格差を数値化する
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
ジニ係数
について紹介します。
よく、
会社全体が支払う給料の80%は上位5%に支払われる
(数字は架空のものです)
など聞いたことありませんか?
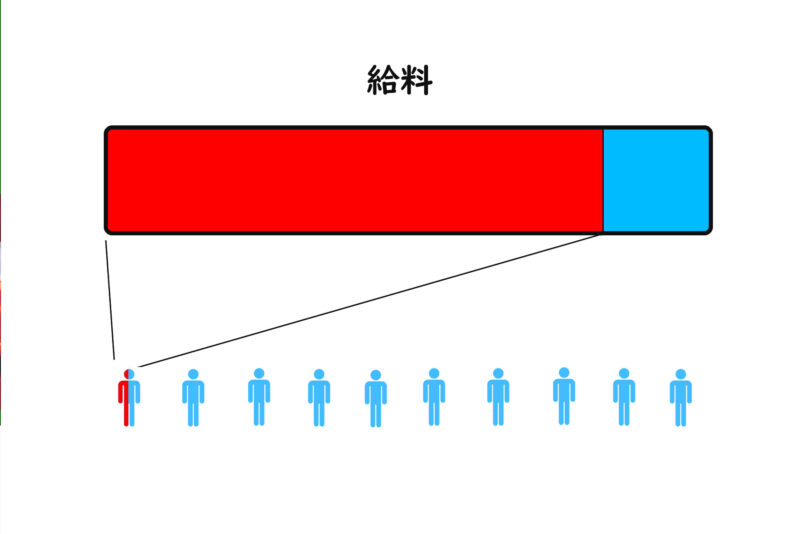
この数字でいくと、
残りの20%を95%の人で分けていることになりますよね。
このようなものを
格差
と言います。
完全に均等とはいかないにしても、
広すぎる格差は不均等ですよね。
今回は、そんな格差を数値で表した
ジニ係数
についての説明です。
それでは、よろしくお願いします。
ジニ係数
ジニ係数とは
ジニ係数とは、
格差を数値で表したもの
です。
「会社全体の給料の格差」「日本の所得格差」
を見る時などに使用されています。
よく、
会社全体が支払う給料の80%は上位5%に支払われる
(数字は架空のものです)
などのような話を聞きますよね。
このように、全体の配分が均衡か不均衡か見るものを
格差
と言います。
格差が、
小さい
均衡
大きい
不均衡
となります。
均衡とは同じという意味ではありません。
均衡と平等は違います。
どんな値になる?
ジニ係数は、
0 ~ 1までの値
になります。
ジニ係数が
0に近い
均衡
1に近い
不均衡
となります。
どんな時に使用する?
ジニ係数の使い方としては、主に
- 値を見て格差具合を調べる
- 複数のジニ係数を比較してどちらの方が格差があるかを調べる
などがあります。
値を見て格差具合を調べる
ジニ係数は、格差を数値化したものです。
つまり、その数値自体が格差具合を表しています。
ジニ係数が、
0に近い
格差が少ない
1に近い
格差が大きい
となります。
私の中では0.3以上はなかなか格差があると思われます。
このようなローレンツ曲線があったとします。
こちらのジニ係数を求めると、
0.32
となります。
求め方は下で紹介します。
全体の約1/3であるため、格差は少ないように見せますよね。
しかし実際には、
全体の上位20%が全体の50%を占めている
のです。
そう考えると格差がないと少ないとは言えませんよね。
複数のジニ係数を比較してどちらの方が格差があるかを調べる
ジニ係数には、単位がありません。
そのため、他の値との比較に非常に便利です。
複数のジニ係数を比較し、
どちらの方が格差が大きいか・どちらの方が格差が小さいか
を調べることができます。
ジニ係数が大きいほど、格差も大きいです。
使用するもの
ジニ係数を求めるには、
ローレンツ曲線
を使用します。
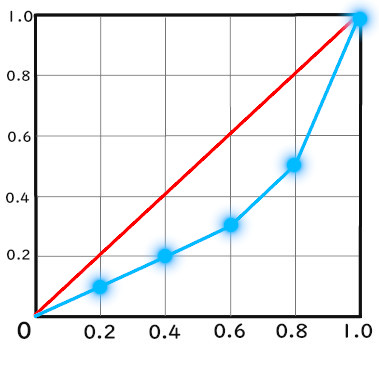
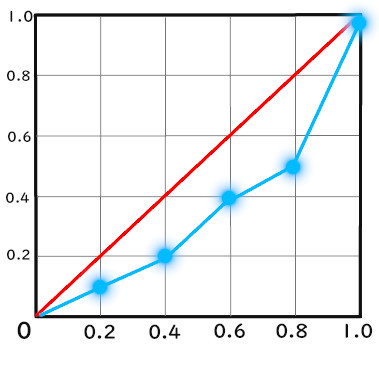
ローレンツ曲線
ローレンツ曲線とは、
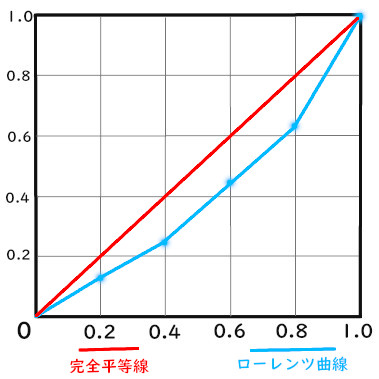
このような曲線のことです。
曲がっている線のことをローレンツ曲線と言います。
実際には、
ローレンツ曲線が完全平等線とどのくらい離れているかを見る
ために使用します。
ローレンツ曲線ついてはこちらで紹介させていただいています
よろしかったらどうぞ
考え方
ジニ係数とは、
「1×1の直角三角形」に対する「ローレンツ曲線と完全平等線の中」の割合
です。
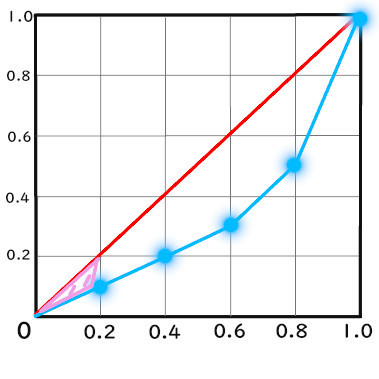
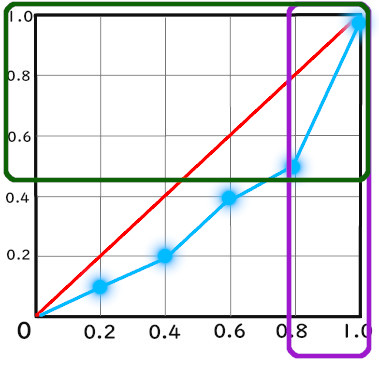
1×1の直角三角形
まず「1×1の直角三角形」について見てみましょう。
「1×1の直角三角形」とは、
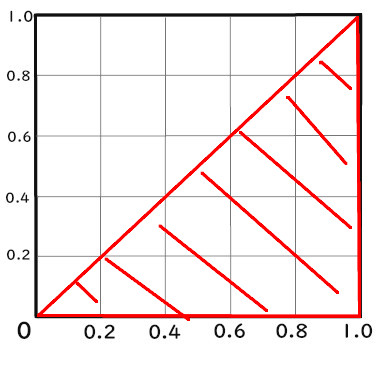
こちらのことです。
単純にローレンツ曲線が入っている側の
三角形になります
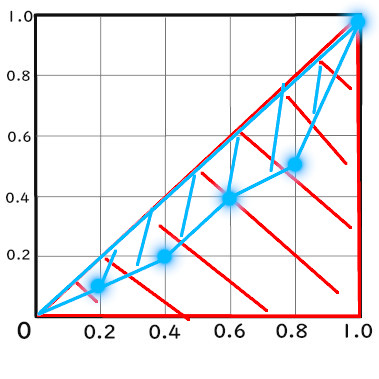
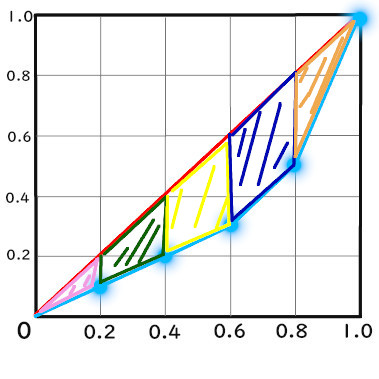
ローレンツ曲線と完全平等線の中
次は、「ローレンツ曲線と完全平等線の中」について見てみましょう。
「ローレンツ曲線と完全平等線の中」とは、
こちらのことです。
中の三日月のような形のことです。
求め方
ジニ係数の求め方は、
中の面積 × 2
です。
単純に面積を２倍すれば求められます。
なぜこの求め方になるの?
先ほども書きましたが、ジニ係数は、
「1×1の直角三角形」に対する「ローレンツ曲線と完全平等線の中」の割合
です。
ここで、「1×1の直角三角形」の面積を見てみましょう。
この三角形は、底辺：1・高さ：1の三角形ですね。
そのため面積は、
底辺 × 高さ ÷ 2
= 1 × 1 ÷ 2
= 1/2
となります。
そしてジニ係数は、「1×1の直角三角形」に対する「ローレンツ曲線と完全平等線の中」の割合のため、
中の面積 ÷ 1/2
となります。
それを計算すると、
中の面積 ÷ 1/2
= 中の面積 × 2
よってこの式で割合が求められます。
例
| 横軸 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
| 縦軸 | 0.1 | 0.2 | 0.3 | 0.5 | 1.0 |
こちらのローレンツ曲線からジニ係数を求めましょう。
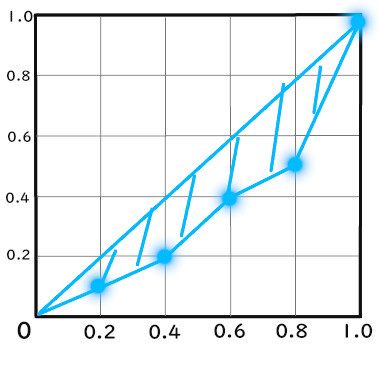
1、中を分ける
まずは、中の面積を求めましょう。
その場合、こちらのローレンツ曲線を
このように分けます。
分けることで、三角形と台形に分かれましたね。
2、各面積を求める
では、一つづつ求めましょう。
2.1、0 ~ 0.2までの面積
三角形の面積になります。
\(( 0.2 – 0.1 ) × 0.2 ÷ 2\)
\(= 0.01\)
よって、
0.01
です。
2.2、0.2 ~ 0.4までの面積
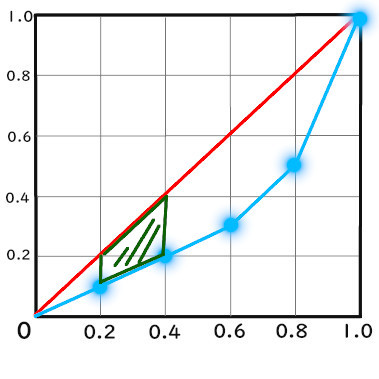
台形の面積になります。
\({ ( 0.2 – 0.1 ) + ( 0.4 – 0.2 ) } × 0.2 ÷ 2\)
\(= 0.03 \)
よって、
0.03
です。
2.3、0.4 ~ 0.6までの面積
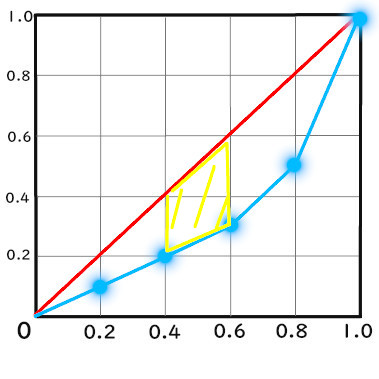
台形の面積になります。
\({ ( 0.4 – 0.2 ) + ( 0.6 – 0.4 ) } × 0.2 ÷ 2\)
\(= 0.04 \)
よって、
0.04
です。
2.4、0.6 ~ 0.8までの面積
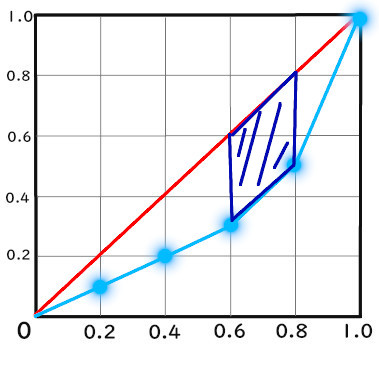
台形の面積になります。
\({ ( 0.6 – 0.3 ) + ( 0.8 – 0.5 ) } × 0.2 ÷ 2\)
\(= 0.04 \)
よって、
0.06
です。
2.5、0.8 ~ 1.0までの面積
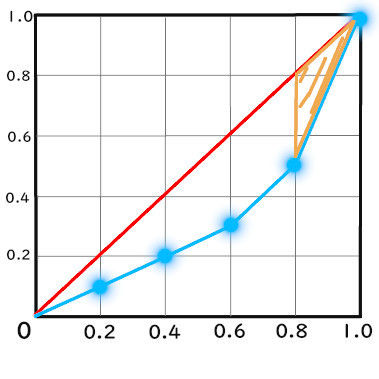
台形の面積になります。
\(( 0.8 – 0.5 ) × 0.2 ÷ 2\)
\(= 0.04 \)
よって、
0.03
です。
3、中の面積を求める
それでは中の面積を求めます。
つまり、今求めた面積の合計を求めましょう。
\(0.01 + 0.03 + 0.04 + 0.06 + 0.03\)
\(= 0.17 \)
よって、中の面積は、
0.17
です。
4、2倍する
あとは、2倍すればジニ係数が求めまられます。
\(0.17 × 2\)
\(= 0.34 \)
よって、
ジニ係数は0.34
と求めることができました。
まとめ
今回、
ジニ係数
について紹介させていただきました。
ジニ係数とは、
データの格差を数値化したもの
です。
ジニ係数を求めるために必要なのは、
ローレンツ曲線
です。
ジニ係数を求めることで、
- 値を見て格差具合を調べる
- 複数のジニ係数を比較してどちらの方が格差があるかを調べる
などがあります。
主に複数のジニ係数の比較に使用します。
格差を調べることで、
全体の中の格差を知る
ことができます。
4等分して、
- 下位25%にどのくらいあるのか
- 真ん中の50%にどのくらい集まっているのか
などを知ることができます。
最後まで読んでいただき、ありがとうございました。
コメント