平均からの歪み具合
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
統計学で扱われる代表的な値の一つに
歪度
というものがあります。
こちらは、
各値を棒グラフでグラフ化したときに平均からどちら側によっているか
を表す値です。

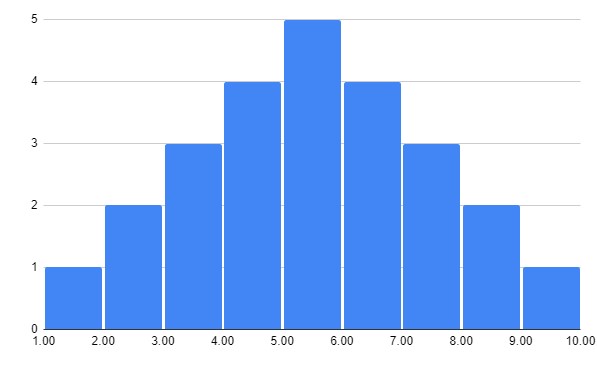
ちなみに左右対称なら歪度は0です。
分布を比較するとき、大体は平均値・分散・標準偏差で比較をします。

真ん中かそこからのズレですね。
しかし、分散が同じでも分布の異なることもあります。
例えば、
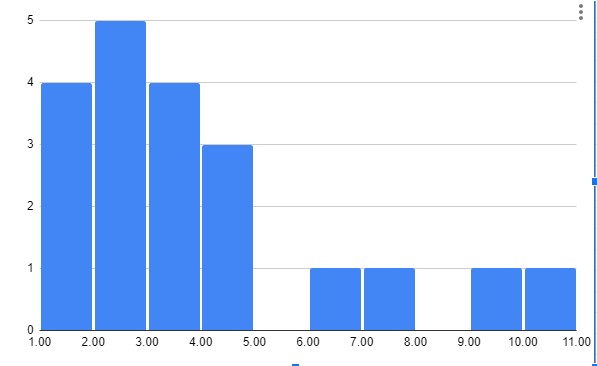
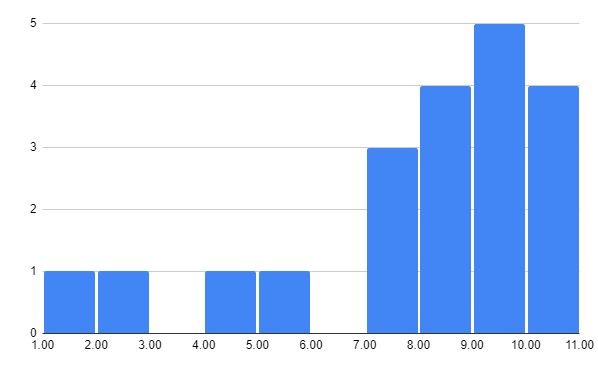
この二つのグラフ
です。
どちらも平均からのズレが同じです。
異なるのは、
ズレの方向
です。

右に大きくズレているか
左に大きくズレているかです。
それを調べることのできる値が
歪度
です。
歪度を調べることで、
値が平均よりどちら側に多い傾向があるか
を知ることができ
それでは、よろしくお願いします。
歪度
説明
歪度とは
歪度とは、
各値の分布の非対称性を表す値
になります。
つまり、
棒グラフにしたとき平均からどちら側に値がよっているか
を表す値ということです。

どっちによってるかな?
どんなときに使用するの?
歪度は、
分布が平均からどちらに多い傾向があるかを知りたいとき
に使用します。
正規分布は主に、
平均値・分散・標準偏差
などで比較をします。
しかしこれらの値は、左右の違いを比較できません。

どのくらい離れているかなどの値です。
そのため、
値が平均から左右のどちら側に多いかを知りたい
ときに使用します。
何がわかる?
歪度を使用することで、
- 平均値から左右対称
- 平均より大きい値がある傾向
- 平均より小さい値がある傾向
のどれなのかを知ることができます。
調べ方
歪度を求めると、
歪度 < 0
歪度 = 0
歪度 > 0
のどれかになります。
その値によって、
と傾向がわかるようになります。

大きいか小さいかを
間違えないように気をつけましょう。
公式
歪度は、
確率変数の場合
\(\dfrac{E\left( \left( X-\mu \right) ^{3}\right) }{\sigma ^{3}}\)
\(E\left( X\right)\)
:Xの期待値
\(X\)
:各値
\(\mu\)
:平均値
\(\sigma\)
:標準偏差
データの場合
\(\dfrac{1}{n}\dfrac{\sum ^{n}_{i=1}\left( x_{i}-\overline{x}\right) ^{3}}{s^{3}}\)
\(n\)
:データ数
\(x_{i}\)
:各値
\(\overline{x}\)
:平均値
\(s\)
:標準偏差
で求められます。
各値-平均を3乗することにより、
- マイナスなら「歪度も-」に影響する
- プラスなら「歪度も+」に影響する
ようになります。

3乗することで-は-のままですからね。
それに3乗することで1と2の間でも大きな違いができます。
まとめ
今回、
歪度
について紹介させていただきました。
歪度とは、
分布の値が平均から左右のどちら側に多いかを知りたい
ときに使用します。
分布を比較するとき、大体は平均値・分散・標準偏差で比較をします。

真ん中かそこからのズレですね。
しかし、平均値・分散・標準偏差共に同じでもまだ全然違う分布であることがありえます。
そんなときに使用するのが、歪度です。
歪度を調べることで、
値が平均よりどちら側に多い傾向があるか
を知ることができます。
最後まで読んでいただき、ありがとうございました。



コメント