平均からの尖り具合
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
統計学で扱われる代表的な値の一つに
尖度
というものがあります。
こちらは、
各値をグラフ化したときに平均周りにあるか
を表す値です。
ちなみに正規分布が0です。
分布を比較するとき、大体は平均値・偏差から比較をします。
真ん中かそこからのズレですね。
そんな時、
分布の形が全然違うのに分散だけで比較して良いのかなぁ?
などと思うことがあります。
そんな時に調べる値が
尖度
です。
尖度を調べることで、
値が平均近くか遠くどちらに多い傾向があるか
を知ることができます。
それでは、よろしくお願いします。
尖度
説明
尖度とは
尖度とは、
各値の分布の尖り具合を表す値
になります。
つまり、
グラフ化したとき平均周りに値が多いか平均より遠い位置に値が多いか
を表す値ということです。
グラフの先端は尖ってるかな?
どんなときに使用するの?
尖度は、
各分布が正規分布に比べて平均近くに多いか遠くに多いかを判断する時
に使用します。
分布は主に、
平均値・分散・標準偏差
などで比較をします。
その中で平均近くか遠くを比べるとなると、偏差や分散を使います。
しかし、分布にも正規分布っぽい形もあればそうでない形もあります。
その二つの分布を分散などで比較しても難しいです。
そのような時、尖度を使用して正規分布に対する尖り具合を調べることで、お互いのズレ具合の比較ができます。
どちらも対象を正規分布にすることで、比べやすくなります。
そのため、
- 一つの分布の各データが平均近くによっているか遠くによっているかを調べる
- 複数の分布でどちらの方が平均近くにあるかを比べる
ときなどに使用します。
何がわかる?
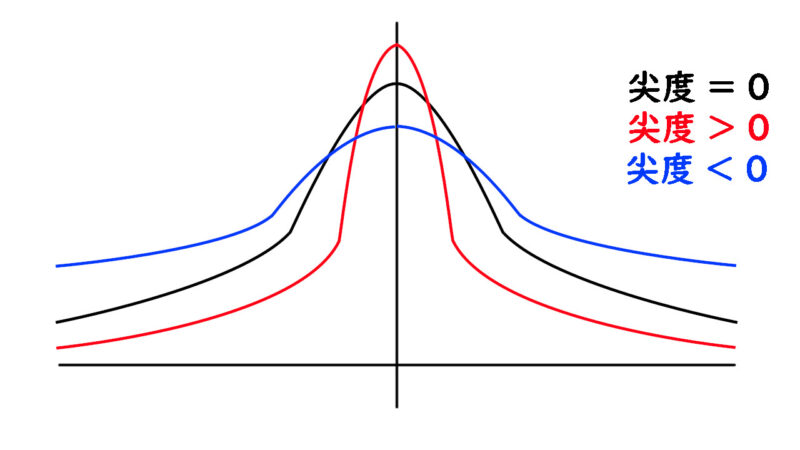
尖度を使用することで、
- 各値が平均付近に多い傾向
- 各値が平均より遠くが多い傾向
のどれなのかを知ることができます。
調べ方
尖度を求めると、
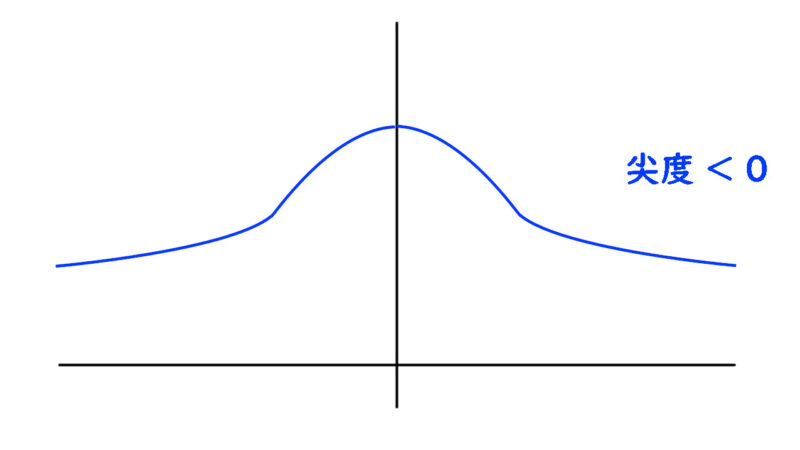
尖度 < 0
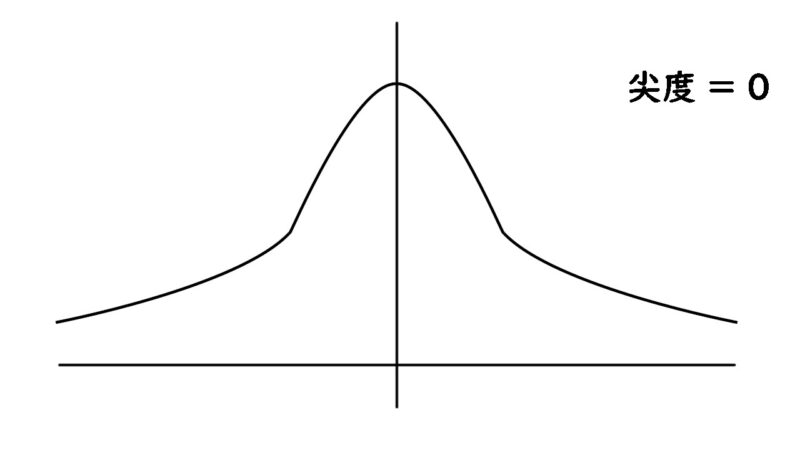
尖度 = 0
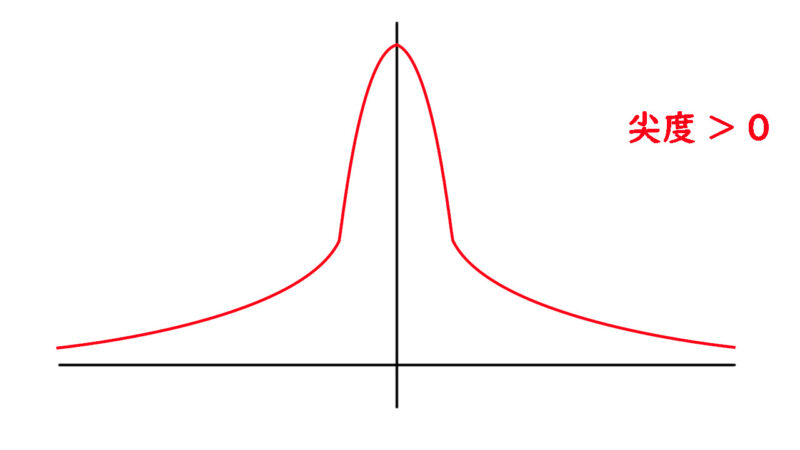
尖度 > 0
のどれかになります。
その値によって、
尖度 < 0
正規分布より遠くに多い
尖度 = 0
正規分布と一緒
尖度 > 0
正規分布より近くに多い
と傾向がわかるようになります。
大きいか小さいかを
間違えないように気をつけましょう。
公式
尖度は、
確率変数の場合
\(\dfrac{E\left( X-\mu \right) ^{4}}{\sigma ^{4}}-3\)
\(E\left( X\right)\)
：Xの期待値
\(X\)
：各値
\(\mu\)
：平均値
\(\sigma\)
：標準偏差
データの場合
\(\dfrac{\dfrac{1}{n}\sum ^{n}_{i=1}\left( x_{i}-\overline{x}\right) ^{4}}{s^{4}}-3\)
\(n\)
：データ数
\(x_{i}\)
：各値
\(\overline{x}\)
：平均値
\(s\)
：標準偏差
で求められます。
各値-平均を4乗することにより、
- 符号による向きが関係なくなる
- 近くの値の影響が小さくなり、遠くの値の影響が大きくなる
ようになります。
4乗することで-は符号+なります。
それに4乗することで1と2の間でも大きな違いができます。
また、なぜ-3をするのかというと、
-3をすることで正規分布が0になるから
です。
正規分布の尖度=0にすることで
正規分布との比較をしやすくします。
まとめ
今回、
尖度
について紹介させていただきました。
尖度とは、
正規分布と比較して各値が平均近くによっているか遠くによっているかを調べたい
ときなどに使用します。
分布を比較するとき、大体は平均値・分散・標準偏差で比較をします。
真ん中かそこからのズレですね。
その中、
平均が同じだから分散で比較しよう
と考えることもあります。
しかし、分布が正規分布っぽいかそうでないかで分散だけでは比較しづらいです。
全く形が違うのにズレだけで比較して良いのかな?
そのような時に尖度を使用しましょう。
尖度を使用することで、
- 正規分布より近い値が多い
- 正規分布より遠い値が多い
などがわかるようになります。
最後まで読んでいただき、ありがとうございました。
コメント