二つのデータの関係を見つける図
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
散布図
について勉強していこうと思います。
散布図
散布図とは二つの項目のあった箇所に点をつける図
散布図とは、
縦軸・横軸にデータの別の項目を当てて、二つの項目が当てはまる箇所に点を打つグラフ
です。

点を打つことを、”プロットする”とも言います。
用途
散布図は、
二つの項目の関係を見つける
時に使用します。
二つの項目の関係のことを、
相関
と言います。

二つの項目が関係があるなら「相関がある」
ないなら「相関がない」
と言います。
3種類の相関
相関には3パターンあります。
- 正の相関
- 負の相関
- 無相関 (相関がない)
の3パターンです。

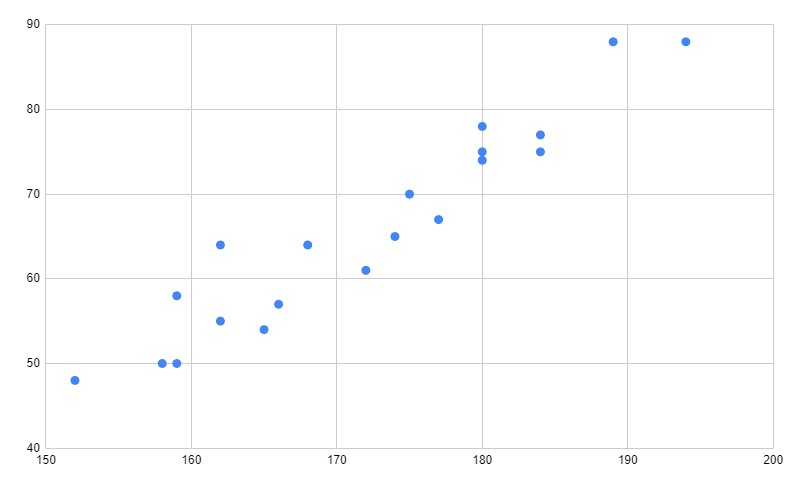
正の相関

このような散布図を、
正の相関
と言います。
特徴は、
一方が増えたらもう一方も増える関係
です。

ある程度のデータを集めて正の相関になったら、
これからも一方が増えたら、もう一方も増えるかも
という推測ができます。
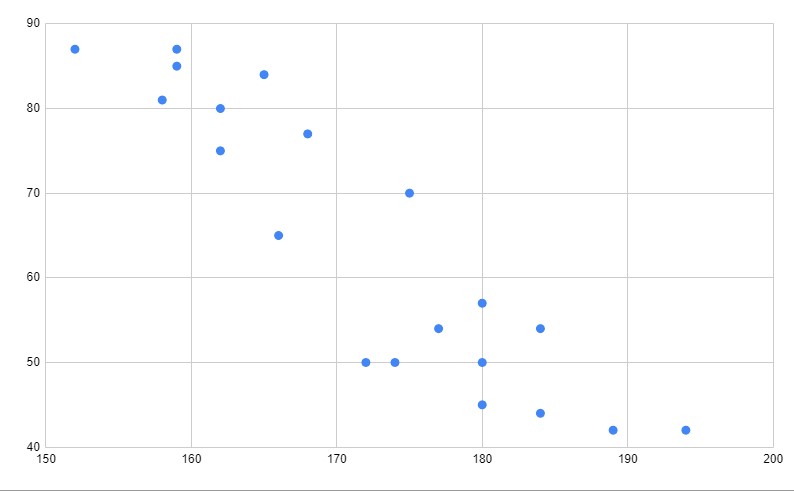
負の相関

このような散布図を、
負の相関
と言います。
特徴は、
一方が増えたらもう一方が減る関係
です。

ある程度のデータを集めて負の相関になったら、
これからも一方が増えたら、もう一方は減るかも
という推測ができます。
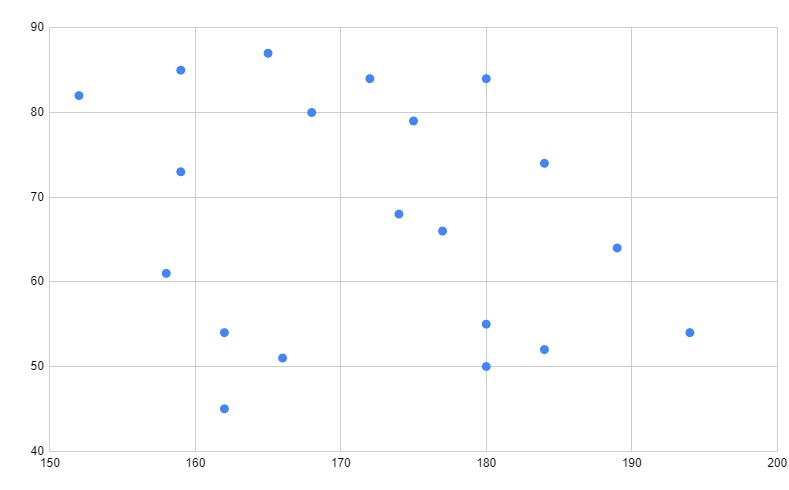
無相関 (相関がない)

このようにバラバラな散布図を、
無相関 または 相関がない
と言います。
特徴は、
二つの項目に関係が見えない
ことです。

ある程度データを集めても関係はないと考えられます。
よって、この図からこれからの推測は難しいです。
書き方
散布図の書き方は、
対応する二つの項目を縦軸と横軸にし、合う箇所に点を打っていくのみ
です。

今は、ExcelやGoogleスプレッドシートに散布図が入っています。
そのため、二つの項目の表を作ればすぐに散布図が作れますよ。
例
身長と体重の関係
身長と体重の関係を例として散布図を作ってみましょう。
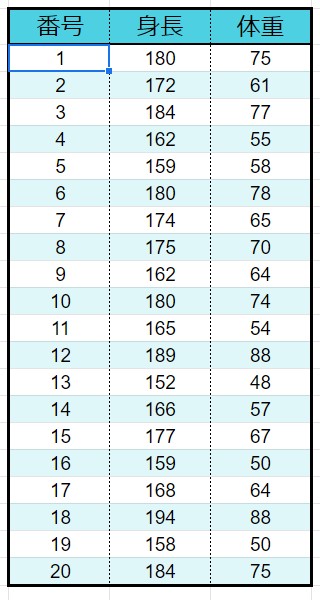
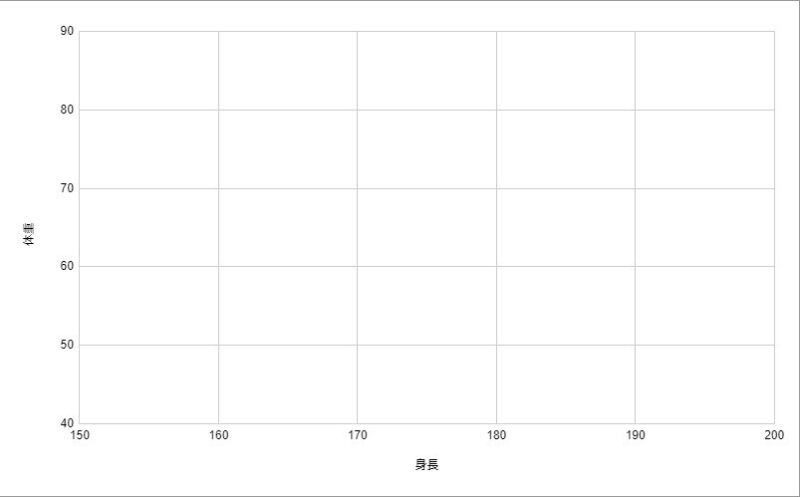
1、1番の項目をグラフにプロット
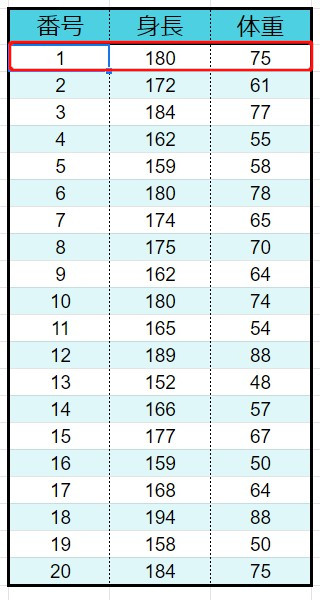
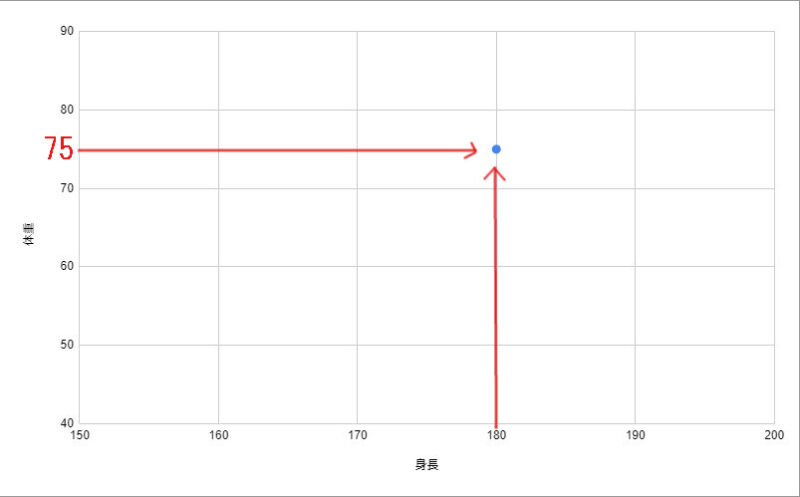
2、2番目の項目をグラフにプロット
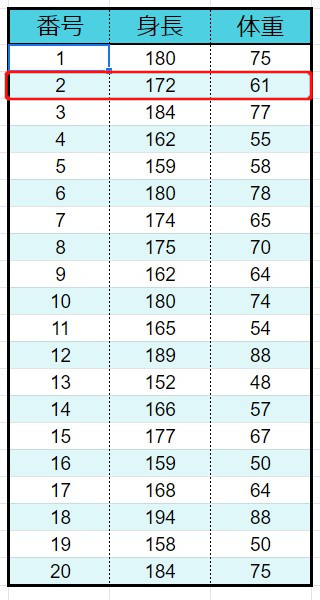
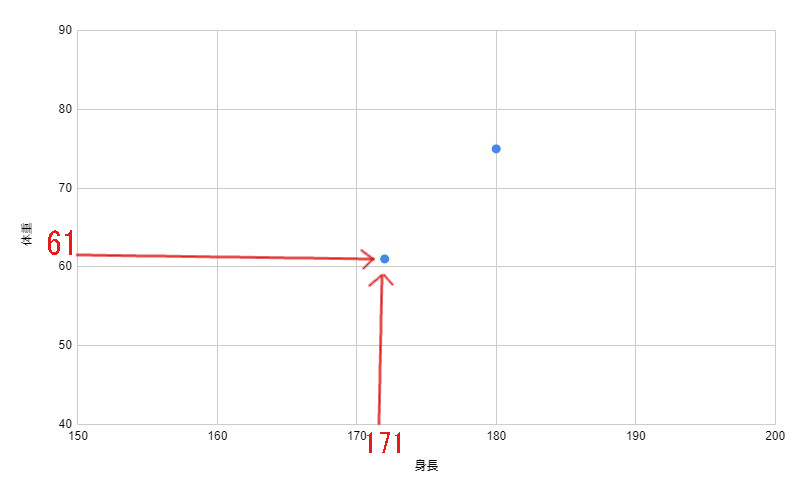
3、3番目の項目をプロット
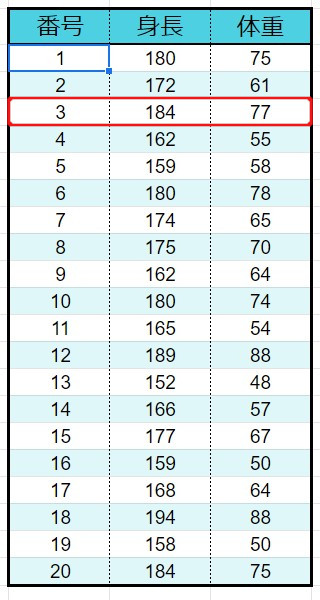
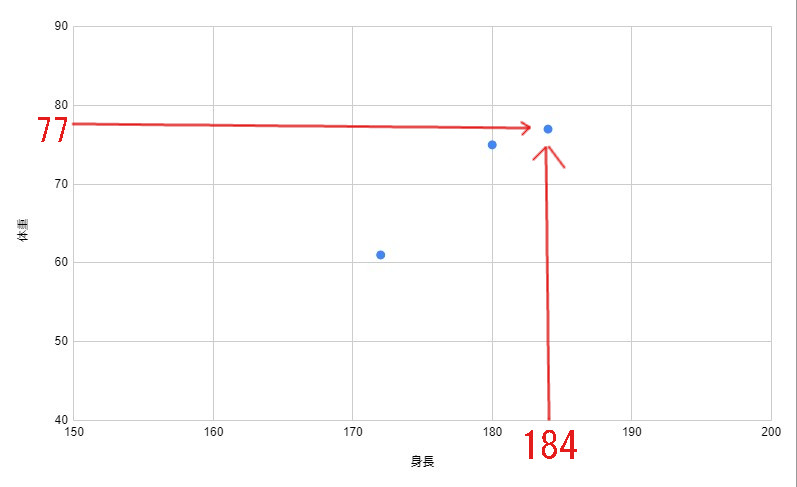

散布図はこのように1項目ずつプロットすることでできます。
4、全ての項目をプロットする
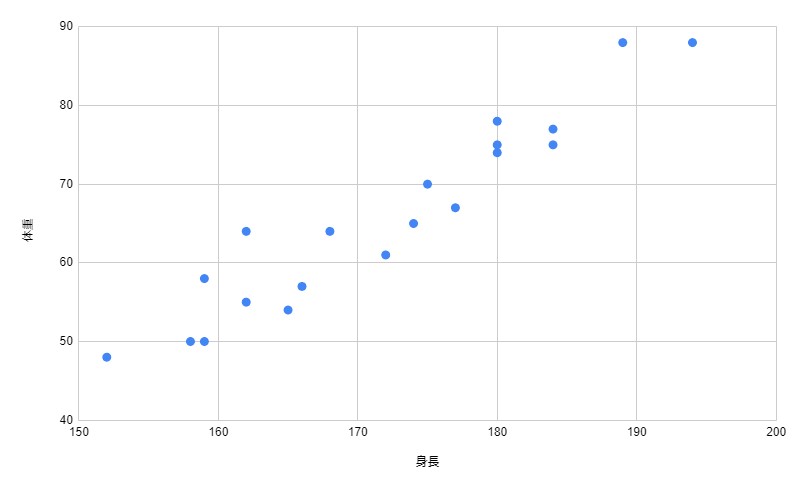

今回は、正の相関になりました。
つまり、身長が高いほど体重も多いと推測できます。
まとめ
今回は、「散布図」について紹介させていただきました。
散布図は、
二つのデータの関係を見つけるためのグラフ
です。
この二つのデータの関係を
相関
と言います。
相関には、
- 正の相関:一方が増えればもう一方も増える
- 負の相関:一方が増えればもう一方は減る
- 無相関 または 相関がない:二つの関係が見えない
の3パターンに分かれます。
これにより、
二つのデータの関係性やこれからのデータの推測
ができるようになります。

統計ですので、ある程度のデータは必要です。
データがあればあるほど精度は上がります。
最後まで読んでいただき、ありがとうございました。



コメント