偏差積和(2つのデータのバラツキを掛けた総和)の平均
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
共分散
について勉強していこうと思います。
共分散
共分散とはバラツキを掛けた総和の平均
共分散とは、
2つのデータ項目を持つデータのバラツキを掛けた総和
です。
- バラツキ → 偏差
- 掛ける → 積
- 総和 → 和
つまり、
偏差積和の平均値
です。
用途は相関係数を求めるときに使用
偏差積和の用途としては、
相関係数を求めるときに使用する
ことがメインです。
また、共分散の値で相関を見ることもできます。
データ項目Xとデータ項目Yの共分散を求める場合、
- 共分散が正の数 → Xが正だとYも正・Xが負だとYも負の傾向にある → 正の相関
- 共分散が0に近い → XとYに傾向がない → 無相関
- 共分散が負の数 →Xが正だとYは負・Xが負だとYは正の傾向にある → 負の相関
と見ることができます。
求め方
公式
共分散の公式は、
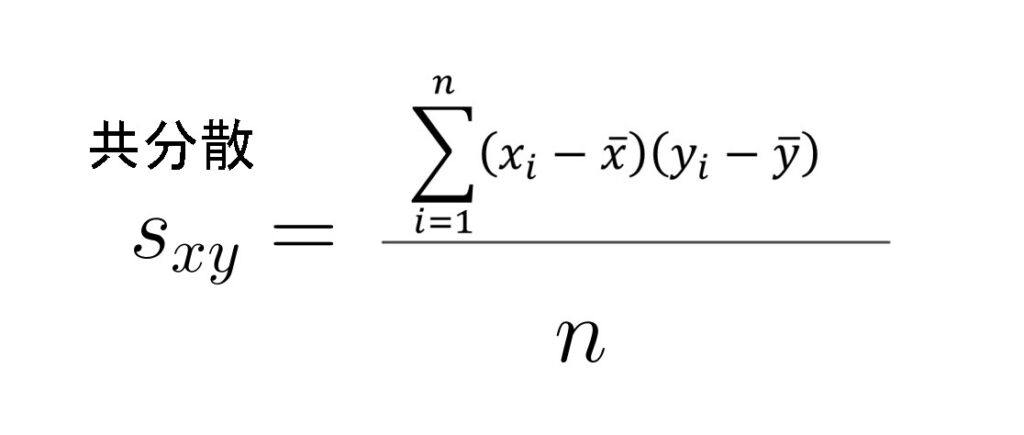
です。

そのまま見てもよくわからないですね。
実際には、上の式は偏差積和です。
また、nとはデータ数になります。
つまり、

となります。
よって、
共分散は偏差積和の平均値
と考えることができます。

平均値なので、偏差積和をデータ数で割るのみですね。
偏差積和
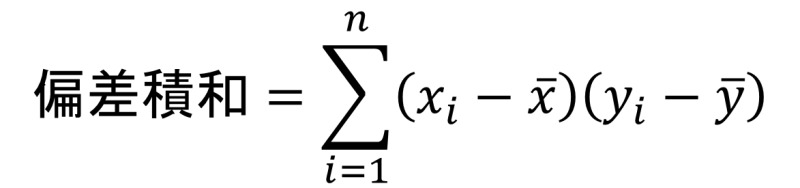
偏差積和については、こちらで紹介しています。
よろしかったらどうぞ
データ数
データ数とは、
データの数
です。

そのままですね。
使用したデータの数を数えましょう。
割る

偏差積和をデータ数で割ります。
ある値をデータ数で割るということは、
その値の平均を求める
ということです。
今回では、ある値:偏差積和です。
よって、
共分散 = 偏差積和の平均を求める
ということになります。
使い方
共分散の使い方は主に、
- 相関係数を求めるときに使用する
- 相関の向きを見る
の2つがあります。

こちらは、偏差積和と同じです。
主な使い方は、
相関係数を求めるときに使用する
です。
相関係数については後日説明させていただきます。
なぜ共分散から相関の向きが見えるのか
共分散は、

で求められます。
下のデータ数は、必ず正の数になります。

データの数がマイナスになるはずがありませんよね。
つまり、
偏差積和の正負で共分散の正負も決まる
ということです。
そして、
- 偏差積和が正 → 正の相関
- 偏差積和が0に近い → 無相関
- 偏差積和が負 → 負の相関
の傾向にあると考えられるため、
共分散も
- 正 → 正の相関
- 0に近い → 無相関
- 負 → 負の相関
と考えられます。
例
身長と体重の関係
身長と体重の関係を例として共分散を求めてみましょう。
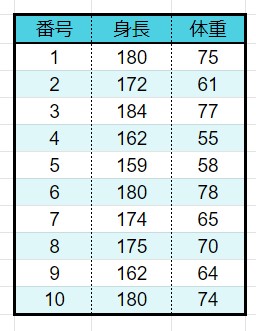
1、2項目の平均を求める
平均は、合計 / データ数です。
身長の平均
(180+172+184+162+159+180+174+175+162+180) / 10 = 172.8
体重の平均
(75+61+77+55+58+78+65+70+64+74) / 10 = 67.7
2、2項目の偏差を求める
偏差は、データ – 平均です。
身長の偏差
180 – 172.8 = 7.2
172 – 172.8 = -0.8
184 – 172.8 = 11.2
162 – 172.8 = -10.8
159 – 172.8 = -13.8
180 – 172.8 = 7.2
174 – 172.8 = 1.2
175 – 172.8 = 2.2
162 – 172.8 = -10.8
180 – 172.8 = 7.2
体重の偏差
75 – 67.7 = 7.3
61 – 67.7 = -6.7
77 – 67.7 = 9.3
55 – 67.7 = -12.7
58 – 67.7 = -9.7
78 – 67.7 = 10.3
65 – 67.7 = -2.7
70 – 67.7 = 2.3
64 – 67.7 = -3.7
74 – 67.7 = 6.3
3、項目づつの偏差積を求める
お互いの項目を掛けます。
7.2 × 7.3 = 52.56
-0.8 × -6.7 = 5.36
11.2 × 9.3 = 104.16
-10.8 × -12.7 = 137.16
-13.8 × -9.7 = 133.86
7.2 × 10.3 = 74.16
1.2 × -2.7 = -3.24
2.2 × 2.3 = 5.06
-10.8 × -3.7 = 39.96
7.2 × 6.3 = 45.36
4、全ての偏差積の和を求める
和のため、全てを足します。
52.56 + 5.36 + 104.16 + 137.16 + 133.86 + 74.16 + (-3.24) + 5.06 + 39.96 + 45.36 = 594.4

これで偏差積和が求められました。
正の数のため、この二つは正の相関になると考えられます。
5、データ数を数える
データの数は、10です。

こちらはそのまま数を数えましょう。
6、偏差積和をデータ数で割る
先ほど求めた偏差積和をデータ数で割ましょう。
594.4 ÷ 10 = 59.44

これで共分散が求められました。
正の数のため、この二つは正の相関になると考えられます。
まとめ
今回は、「共分散」について紹介させていただきました。
共分散とは、
偏差積和の平均値
です。
主に、
相関係数を求める
ときに使用します。

偏差積和 → 共分散 → 相関係数
という順番に求めていきます。
また、共分散からも相関の向きを推測することができます。

相関の強さなども見るためにも、できる限り相関係数で向きも見ましょう。
これら値により、
二つのデータの関係性やこれからのデータの推測
ができるようになります。
最後まで読んでいただき、ありがとうございました。



コメント