– (マイナス)なら負・+(プラス)なら正
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
相関係数
について勉強していこうと思います。
相関係数
相関係数とは二つのデータの相関を数値化したもの
相関係数とは、
2つのデータ項目の相関関係を数値化したもの
です。
用途は「相関関係を数値で説明する時に使用」
データや散布図を見て、
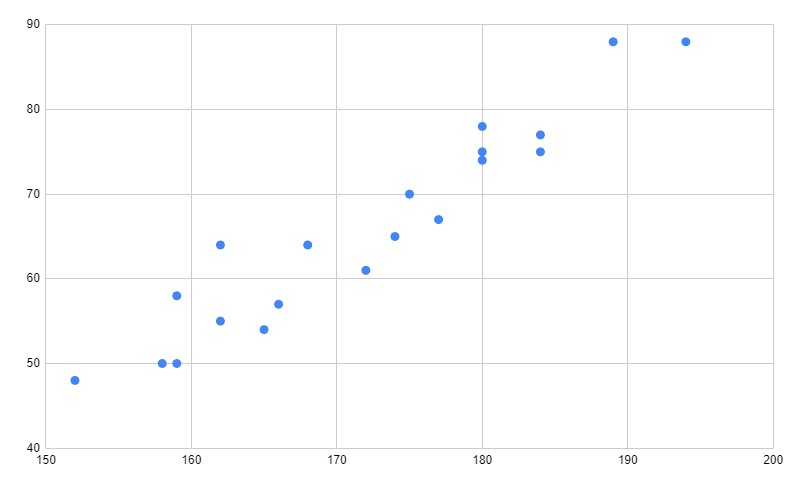

これは正の相関だなぁ。
と考えることができます。
しかし、なぜそうなるのかを上司に聞かれた場合、
散布図を見てそう思った
では理由が弱いですよね。

もっとはっきり言える数値が欲しいですよね。
その時にはっきり言える数値が、
相関係数
です。
つまり、相関係数は
相関関係を数値で説明する時に使用
します。
散布図で視覚化・相関係数で数値化
と考えましょう。
偏差平方和・共分散との違い
相関を数値化できる値として、
偏差積和・共分散
もあります。

この二つも値で相関の向きがわかります。
しかし、相関関係を数値化する場合、基本は相関係数を使います。
なぜなら、偏差積和・共分散は
相関の向きはわかるが、大きさはわからない
からです。

二つとも、単位がついたままのため、
その単位によって大きさは変わってしまいます。
身長 (cm または m)と体重 (g または kg)
cmとg
正の相関
大
cmとkg
正の相関
中
mとkg
正の相関
小

このように単位を変えるだけで大きさは変化してしまいます。
求め方
公式
相関指数の公式は、
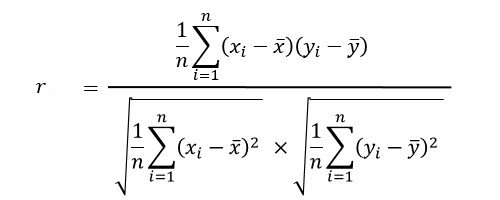
です。

そのまま見てもよくわからないですね。
実際には、分子は共分散・分母はxとyの標準偏差です。
つまり、

となります。
共分散
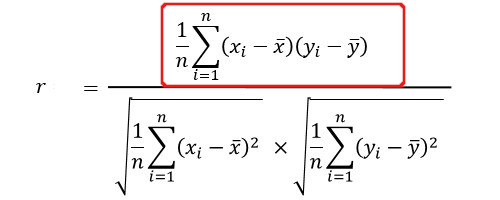
共分散の公式は、
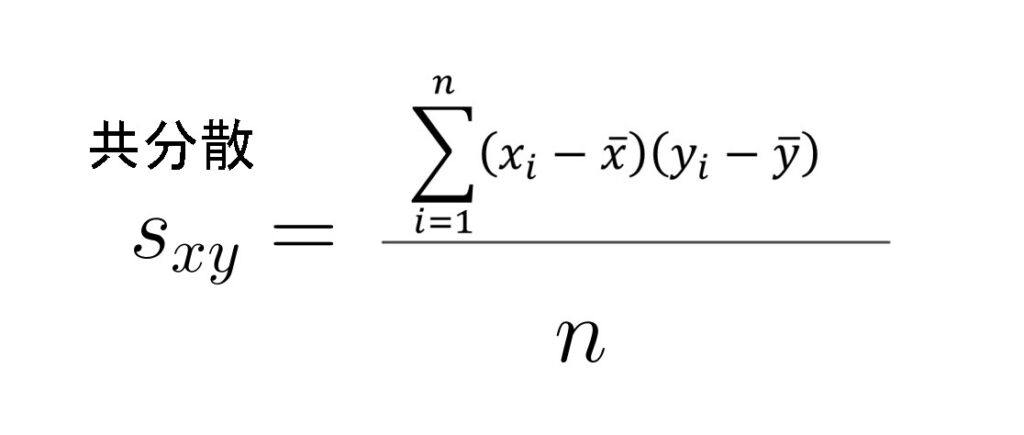
です。
共分散については、こちらで紹介しています。
よろしかったらどうぞ
標準偏差
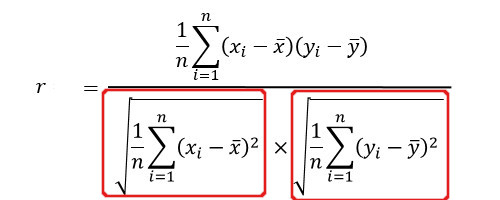
標準偏差の公式は、
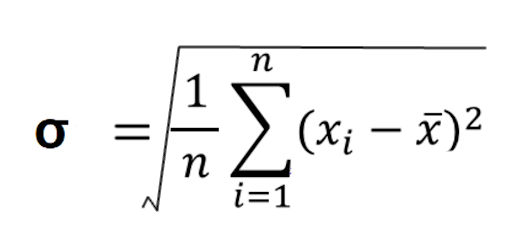
です。
標準偏差については、こちらで紹介しています。
よろしかったらどうぞ
割る
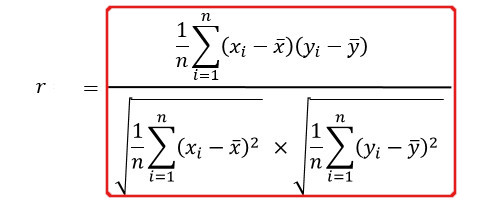

これで相関係数が求められます。
使い方
相関係数の使い方は主に、
二つのデータの相関の向きと強さ
を見つけることです。
向きは+か-か
相関係数は、
-1 ≦ r ≦ 1
の範囲になります。
-1 ≦ r < 0
負の相関
r = 0
無相関
0 < r ≦ 1
正の相関
つまり、
+ か – か 0 かで相関の向きがわかる
のです。
強さは数値の大きさ
強さは
数値の大きさでわかる
のです。
0に近い
相関が弱い
1や-1に近い
相関が強い
となります。
r = -0.732なら、
向き
-のため:負の相関
強さ
0.732のため:強い相関
よって、
強い負の相関の傾向がある
と言えます。
例
身長と体重の関係
身長と体重の関係を例として共分散を求めてみましょう。
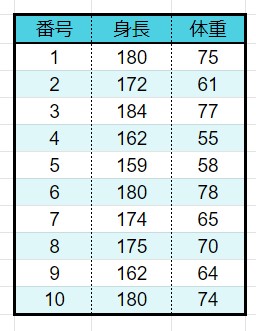
1、共分散を求める
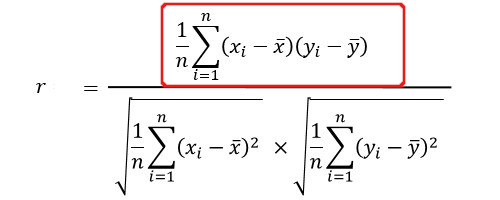
1.1、2項目の平均を求める
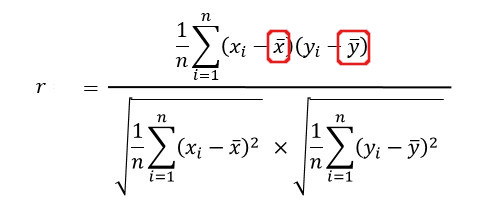
平均は、合計 / データ数です。
身長の平均
(180+172+184+162+159+180+174
+175+162+180) / 10 = 172.8
体重の平均
(75+61+77+55+58+78+65
+70+64+74) / 10 = 67.7
1.2、2項目の偏差を求める
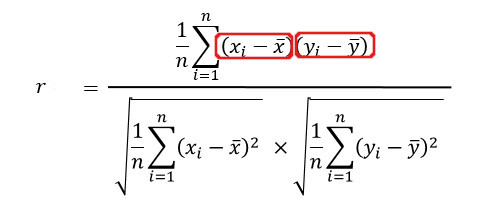
偏差は、データ – 平均です。
身長の偏差
180 – 172.8 = 7.2
172 – 172.8 = -0.8
184 – 172.8 = 11.8
162 – 172.8 = -10.8
159 – 172.8 = -13.8
180 – 172.8 = 8.2
174 – 172.8 = 1.8
175 – 172.8 = 2.2
162 – 172.8 = -10.8
180 – 172.8 = 7.2
体重の偏差
75 – 67.7 = 7.3
61 – 67.7 = -6.7
77 – 67.7 = 9.3
55 – 67.7 = -12.7
58 – 67.7 = -9.7
78 – 67.7 = 10.3
65 – 67.7 = -2.7
70 – 67.7 = 2.3
64 – 67.7 = -3.7
74 – 67.7 = 6.3
1.3、項目づつの偏差積を求める
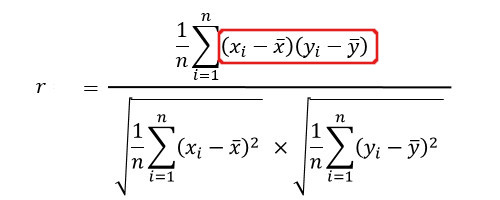
お互いの項目を掛けます。
7.2 × 7.3 = 52.56
-0.8 × -6.7 = 5.36
11.8 × 9.3 = 109.74
-10.8 × -12.7 = 137.16
-13.8 × -9.7 = 133.86
8.2 × 10.3 = 84.46
1.8 × -2.7 = -4.86
2.2 × 2.3 = 5.06
-10.8 × -3.7 = 39.96
7.2 × 6.3 = 45.36
1.4、全ての偏差積の和を求める
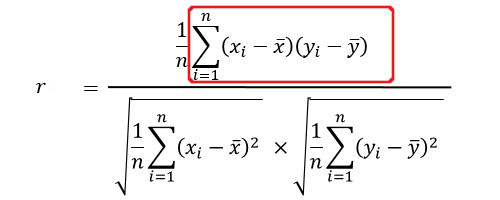
和のため、全てを足します。
52.56 + 5.36 + 109.74 + 137.16 + 133.86 + 84.46 + (-4.86) + 5.06 + 39.96 + 45.36 = 608.66

これで偏差積和が求められました。
正の数のため、この二つは正の相関になると考えられます。
1.5、データ数を数える
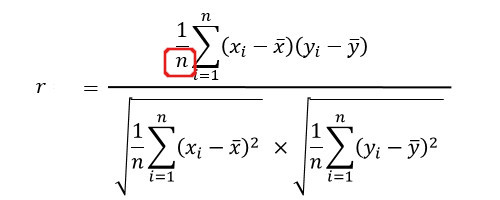
データの数は、10です。

こちらはそのまま数を数えましょう。
1.6、偏差積和をデータ数で割る
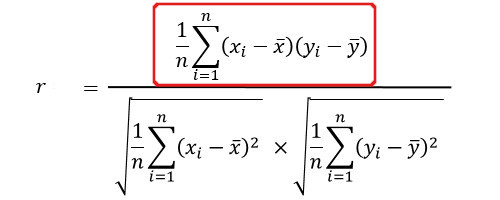
先ほど求めた偏差積和をデータ数で割ましょう。
608.66 ÷ 10 = 60.866

これで共分散が求められました。
2、それぞれの標準偏差を求める
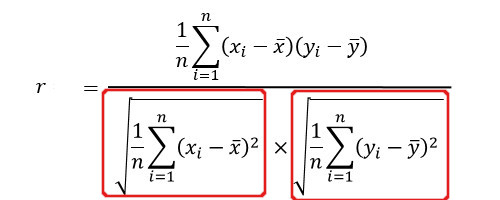
2.1、それぞれの「平均値」を求める
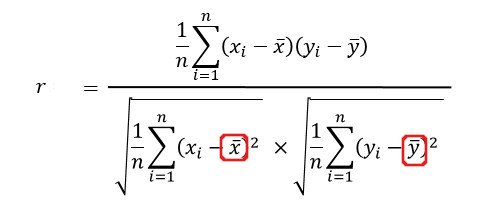
(180+172+184+162+159+180
+174+175+162+180)/10 = 172.8
(75+61+77+55+58
+78+65+70+64+74)/10 = 67.7

こちらは、1.1でも求めましたね。
2.2、それぞれの「偏差」を求める
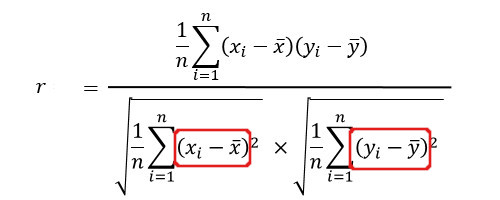
偏差は、
各データの平均との差
です。
身長の偏差
180 – 172.8 = 7.2
172 – 172.8 = -0.8
184 – 172.8 = 11.2
162 – 172.8 = -10.8
159 – 172.8 = -13.8
180 – 172.8 = 7.2
174 – 172.8 = 1.2
175 – 172.8 = 2.2
162 – 172.8 = -10.8
180 – 172.8 = 7.2
体重の偏差
75 – 67.7 = 7.3
61 – 67.7 = -6.7
77 – 67.7 = 9.3
55 – 67.7 = -12.7
58 – 67.7 = -9.7
78 – 67.7 = 10.3
65 – 67.7 = -2.7
70 – 67.7 = 2.3
64 – 67.7 = -3.7
74 – 67.7 = 6.3

こちらも1.2で求めましたね。
2.3、それぞれの「偏差平方和」を求める
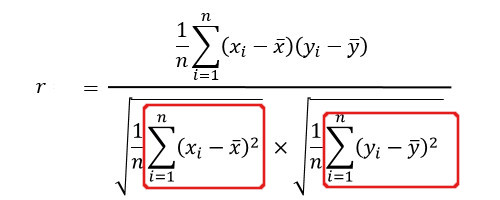
偏差平方和は、
各偏差の2乗の合計
です。
(7.2)2+(-0.8)2+(11.2)2+(-10.8)2+(-13.8)2
+(7.2)2+(1.2)2+(2.2)2+(-10.8)2+(7.2)2
=711.6
(7.3)2+(-6.7)2+(9.3)2+(-12.7)2+(-9.7)2
+(10.3)2+(-2.7)2+(2.3)2+(-3.7)2+(6.3)2
=612.1
2.4、それぞれの「分散」を求める
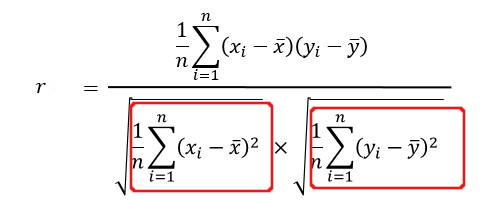
分散は、
偏差平方和 / データの数
です。
711.6 / 10 = 71.16
612.1 / 10 = 61.21
2.5、それぞれの「標準偏差」を求める

標準偏差は、
√分散
です。
√71.16 ≒ 8.44
√61.21 ≒ 7.82
3、二つの標準偏差をかける
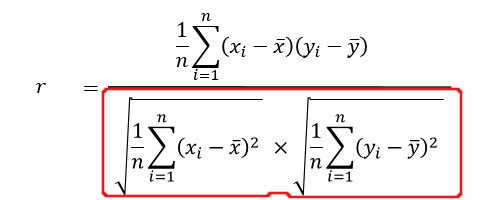
8.44 × 7.82 = 66.0008
4、共分散を標準偏差の積で割る
60.866 / 66.0008 ≒ 0.9222

これで相関係数が求められました。
まとめ
今回は、「相関係数」について紹介させていただきました。
相関係数とは、
2つのデータ項目の相関関係を数値化したもの
です。
主に、
二つのデータ項目の相関の方向と強さを求める
ときに使用します。

偏差積和 → 共分散 → 相関係数
という順番に求めていきます。
この値により、
二つのデータの関係性やこれからのデータの推測
ができるようになります。
最後まで読んでいただき、ありがとうございました。



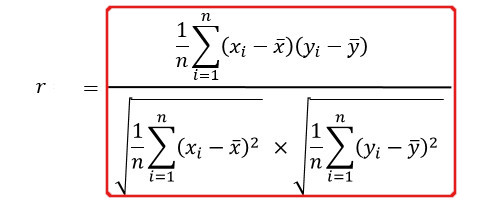


コメント