「疑似相関かも?」を見つけてくれる指標
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
偏相関係数
についてです。
2つのデータ群の関係を求めるとき、どんな値を求めて調べるか覚えていますか?
答えは、
相関係数
です。
相関係数では、
±で向き・値で強さを見つけることができる
のでしたね。
しかし、実際に求めてみて、

この2つ、正の強い相関があるって出たけど、本当になるのかな?
と思うことないですか?
偏相関係数はその疑問を解決するためにあります。
この記事を読めば、
本当に相関があるの?
を解決することができます。

本当に相関があるのか不安になる時ありますよね。
偏相関係数を求めて確認しましょう。
偏相関係数
偏相関係数とは

偏相関係数とは、
2つのデータ群で第三の値の影響を除いた相関係数
です。
つまり、
指定した変数の影響をなくした状態で2つのデータ群がどのような関係なのか
を表す指標です。
なぜ相関係数だけではダメなのか?
二つのデータ群の関係を調べる時、
相関係数の値
で確認することがあります。
その相関係数について問題が一つあります。
それは、
第三の値の影響により2つのデータ群は強い相関がある可能性がある
ということです。
コンビニの数と薬局の数には、強い相関がある
とします
つまり、
「コンビニが多い」と「薬局も多い」傾向にある
ということです。
しかし、本当にコンビニの数と薬局の数に因果関係があるでしょうか?

コンビニが増えたから薬局も増える
とは思わないでしよね。
これは、
近くに住む人の数という第三の値が影響している
と考えられます。
つまり、
コンビニが多いから薬局が多い
のではなく、
人が多いからコンビニが多い
人が多いから薬局が多い
よって、
コンビニと薬局には強い相関関係がある
と考えられる。
このように第三の値による相関なのかを知るための値が
偏相関係数
です。
値の範囲
偏相関係数の値の範囲は、
-1 ≦ r ≦ 1
になります。

もしそれ以外の値になったら計算ミスをしている可能性があります。
見直してみましょう。
使い方
偏相関係数の使い方は主に、
二つのデータの相関の向きと強さ
を見つけることです。

基本的な使い方は、相関係数と同じです。
向きは+か-か
相関係数は、
-1 ≦ r ≦ 1
の範囲になります。
-1 ≦ r < 0
負の相関
r = 0
無相関
0 < r ≦ 1
正の相関
つまり、
+ か – か 0 かで相関の向きがわかる
のです。
強さは数値の大きさ
強さは
数値の大きさでわかる
のです。
0に近い
相関が弱い
1や-1に近い
相関が強い
となります。
つまり、
相関係数
強い
偏相関係数
弱い
だった場合、偽物の相関関係にあると考えられます。
相関係数が-0.732なら、
向き
-のため:負の相関
強さ
0.732のため:強い相関
よって、
強い負の相関の傾向がある
と言えます。
しかし、偏相関係数を求めたら、-0.2でした。
その場合、
向き
-のため:負の相関
強さ
0.2のため:弱い相関
よって、偏相関係数は弱い負の相関を示しているため、
ニセモノの相関関係にあった
と考えられます。

第三の値zのおかげでxとyに相関関係があったと考えられます。
求め方
公式
偏相関係数の公式は、
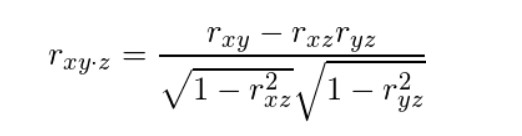
です。

これだけでは、何が何だかわかりませんねw
ゆっくり一つづつ見ていきましょう。
1つ目のデータ群:x
2つ目のデータ群:y
第三の値:z
です。
また、
rは相関係数
ということです。
そのため、
rxy:xとyの相関係数
rxz:xとzの相関係数
ryz:yとzの相関係数
です。
つまり、

ということになります。

3つの相関係数を求めれば、解けるという事ですね。
3つの相関係数を求める
偏相関係数を求めるため、3つの相関係数を求めましょう。
相関係数の公式は、
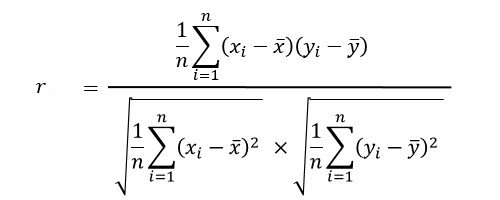
です。
![]() と
と![]() :各データ |
:各データ | ![]() と
と![]() :xとyの平均値 | n:データ数
:xとyの平均値 | n:データ数
相関係数に関してはこちらでも紹介しています
よろしかったらどうぞ

3つの相関係数を求めたら、あとは公式に当てはめることで
偏相関係数が求められます。
注意点
偏相関係数は因果関係を示しているわけではない
偏相関係数はあくまで
相関があるかないか
を求める指標です。
因果関係を示すことはできません。
相関関係も因果関係も
片方が変化すればもう片方も変化する
関係です。
2つ関係の違いは、
相関関係
一方が原因で変化しているわけではない
因果関係
一方が原因で変化している
ということです。
つまり相関関係は、
原因と結果の関係とは限らない
ということです。
まとめ
今回は、
偏相関係数
について紹介させていただきました。
偏相関係数とは、
2つのデータ群で第三の値の影響を除いた相関係数
です。
つまり、
相関係数で求めた相関関係が第三の値による関係であるかないか
を見つけてくれる値です。
求めるのに必要なのは、
3つの相関係数
rxy・rxz・ryz
x:1つ目のデータ群 | y:2つ目のデータ群 | z:第三の値のデータ群
です。

相関係数を求めたら、あとは公式の代入するのみです。
また、偏相関係数の用途は、
相関係数で求めた相関関係が他のデータ群によるものかを確認する
時に使用します。

相関関係を求めたときに、他の値が影響しているのでは?
と思ったら、計算してみましょう。
注意点としては、偏相関係数で求められるのは
相関関係であり因果関係ではない
ということです。

相関関係がある=その値が原因ではないということですね。
最後まで読んでいただき、ありがとうございました。




コメント