相関・相関係数
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
2つのデータ群の比較に使用する指標
について勉強していこうと思います。
2つのデータ群の比較
データ群の比較
たくさんのデータを集めていくと、
お互いのデータの関係を調べたい
ことがあります。
こちらが売れているときはそっちも売れている気がするなぁ
という場合ですね。
実際に、気がするのみで終わってしまってはもったいないですよね。
せっかく、データを集めているのですから、統計学的に調べてみましょう。
使われる指標
2つのデータ群の比較によく使われる指標として、
散布図・相関・偏差積和・共分散・相関係数
というものがあります。
実際に、比較する時によく使われるのは、
相関と相関係数
なります。
しかし、散布図から相関を、そして共分散から相関係数を求めます。
そのため、散布図の書き方や共分散の求め方も学びましょう。
散布図は見たことある方も多いと思います。
また、共分散は二つのデータ群の分散というイメージです。
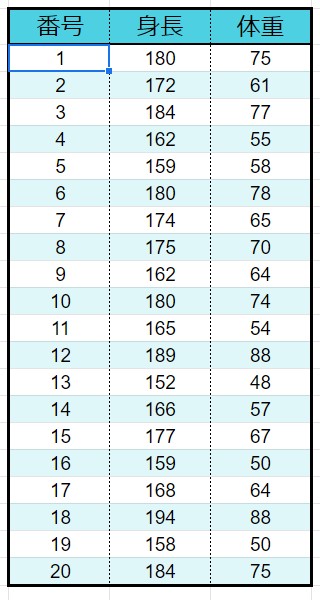
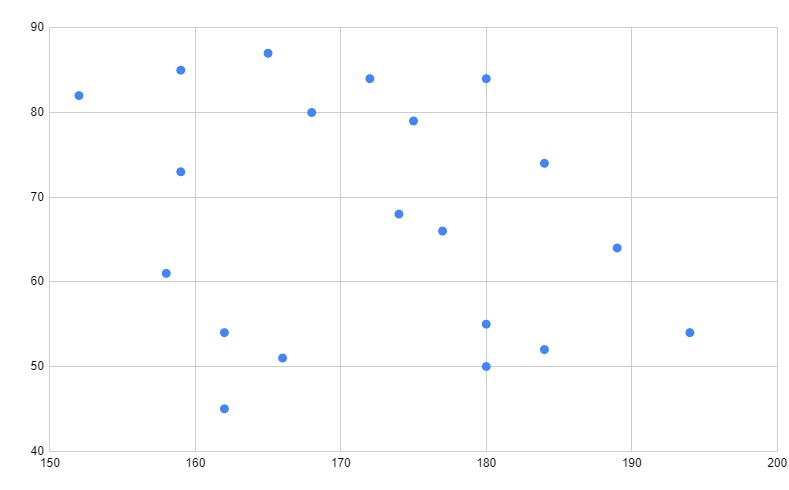
散布図
散布図とは、
二つの項目のあった箇所に点をつける図
です。
点をつけることをプロットするとも言います。
人の身長と体重の関係を散布図にしたものです。
このように、二つの項目の合う箇所をプロットしていきましょう。
他にも、二つの商品の同じ日の売り上げを、数ヶ月分プロットしていき、お互いの商品の関係を調べたりできます。
比較の仕方
散布図での比較の仕方は、
形をみる
のみです。
この散布図の形から
次の相関
を見つけることができるのです。
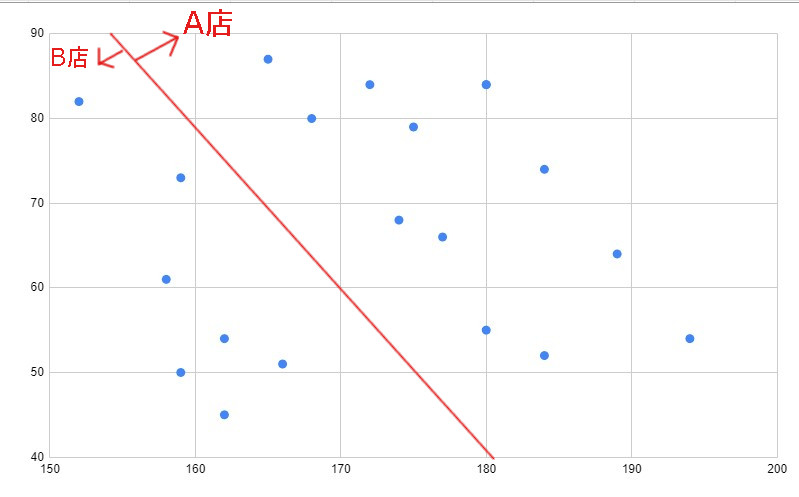
相関
相関とは、
二つの項目の関係
のことです。
二つの項目が、
- 関係があるなら「相関がある」
- 関係がないなら「相関がない」
と言います。
相関は散布図から求める
相関は、
散布図をみることで見つけられる
のです。
なので、二つのデータの関係を知りたい場合は、まず散布図を作りましょう。
相関のパターンは3つ
相関には3つのパターンが存在します。
正の相関
負の相関
無相関
このようにして、どのような関係になるかを見つけましょう。
こちらの散布図はどの相関に見えますか?
こちらを無相関とすぐに見てしまってはいけません。
なぜなら、
このように分けると、二つの負の相関に見えます。
このように、一見無相関に見える場合でも、
他に分け方があれば、相関があるように見える
こともあります。
偏差積和
偏差積和とは、
お互いの偏差の積の和
です。
言葉のままですね。
偏差とは、
各データの平均からの差
です。
偏差ついてはこちらでも紹介しています
よろしかったらどうぞ
片方のデータ：
・平均：
偏差 = ( – )
もう片方のデータ：
・平均：
偏差 = ( – )
このお互いの偏差の積は、
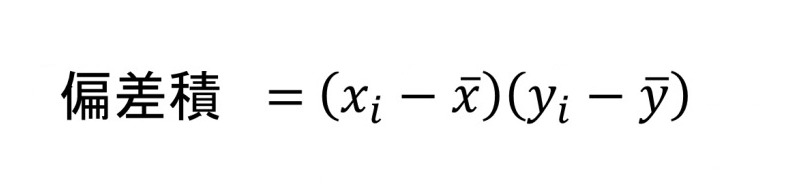
その全ての合計のため、
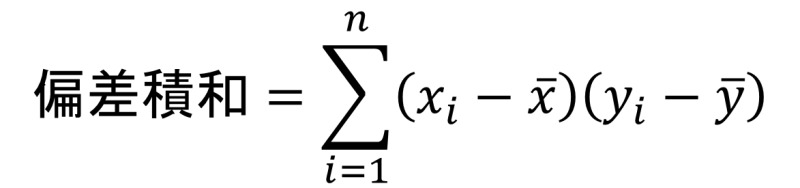
で求められます。
この偏差積和自体は、相関係数を求めるために計算します。
共分散
共分散とは、
偏差積和の平均
です。
つまり、
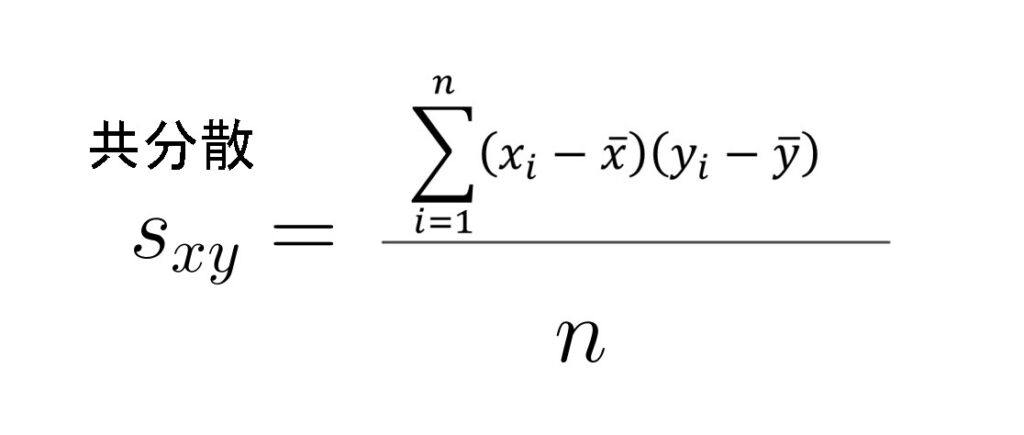
で求めることができます。
共分散は、
- 正の相関の時は、正の値
- 負の相関の時は、負の値
- 無相関の時は、0に近い値
になります。
つまり、共分散からも相関が見つけられます。
しかし、共分散では単位の違う二つのデータを比較することはできません。
そのため、比較する場合は、次の相関係数で比較しましょう。
相関係数
相関係数とは、
相関の強さを比較するための指標
を表します。
相関係数はよく
r
で表されます。
求め方は、
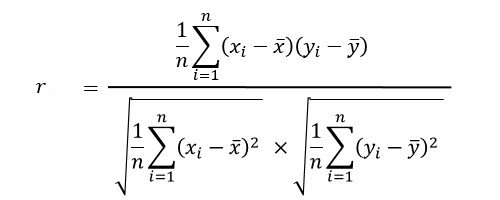
です。
この式だけ見ると、大変そうですね。
しかし、
こうなります。
つまり、
共分散とお互いの標準偏差の3つの値で求めることができる
のです。
比較の仕方 (相関係数)
相関係数rは、
-1 ≦ r ≦ 1
の範囲になります。
- 0 < r ≦ 1 なら正の相関
- -1 ≦ r < 0なら負の相関
- r = 0なら無相関
となります。
まとめ
今回は、
二つのデータ群の関係を調べる指標
について紹介させていただきました。
指標には、
「相関」「相関係数」
などがあります。
「相関」を求めるために、散布図を作ります。
また、「相関係数」を求めるために、
偏差積和・共分散
を求めます。
相関は、散布図から見つけるのが簡単です。
また、いきなり相関係数の求め方を覚えるようりも、
偏差積和 → 共分散 → 相関係数
の順番を理解した方が覚えやすいでしょう。
この指標により、二つのデータの関係を見つけることができます。
最後まで読んでいただき、ありがとうございました。
コメント