各データのバラツキからも違いを比べよう
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
グループA
1・1・2・3・4・5・5
グループB
3・3・3・3・3・3
この複数の集団を比べるときどんな値を求めて比べますか?
平均とかかな
このように複数の集団を比べる時大体平均を求める人が多いと思います。
しかし、平均だけではわからないこともあります。
今回はそんな平均以外で比べられる
バラツキから複数の集団の違いを比べる時の指標
について学びましょう。
バラツキに対しての指標
バラツキとは
バラツキとは、
各データの平均値からの散らばり具合
です。
集団の比較によく使われる指標として、
平均値・中央値・最頻値
があります。
平均値などについてはこちらでも紹介しています
よろしかったらどうぞ
しかし、その値のみでは違いを見つけられないこともたくさんあります。
こちらの二つのグラフは、
平均値：5・中央値：5・最頻値：5
です。
3つの値は同じなのに、
見た目では似ているグラフとは言えないですよね。
このように、代表値と言われる3つの値では違いが分かれない時のために、データのバラツキからも比べます。
実際は、3つの値が同じ場合に求めるのではありません。
3つの値が違っていても、バラツキからも違いを探してみましょう。
使われる指標
バラツキから違いを探すときによく使われる指標として、
偏差・偏差平方和・分散・標準偏差・偏差値
というものがあります。
実際に、比較する時によく使われるのは、
標準偏差と偏差値
なります。
しかし、他の3つから段階的に求めていく方が理解しやすいため、5つとも重要な値になります。
偏差値は見たことや聞いたことがある人もいるのではないでしょうか?
受験の時などに、テストの結果の指標として乗っていることがあります。
偏差
偏差とは、
各データの平均との差
です。
つまり偏差とは、「データ一つ一つが、平均値とどのくらい離れているか」です。
求め方は、
偏差 = 各データ – 平均値
です。
これにより、一つ一つのデータの散らばりを求めます。
偏差についてはこちらでも紹介しています
よろしかったらどうぞ
偏差平方和
偏差平方和とは、
各データのバラツキ具合の合計
です。
計算式のように書くと、
偏差平方和 = 偏差 + 平方 (2乗) + 和 (足す)
ということです。
つまり、
偏差を2乗して足す
ということです。
求め方は、
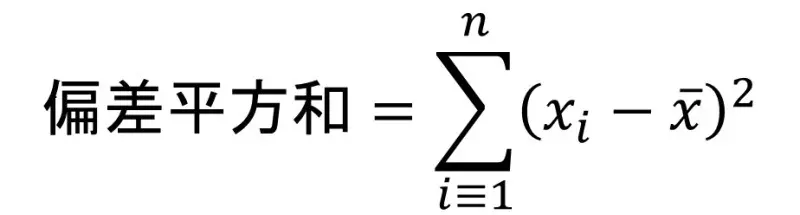
です。
これにより、平均からの距離の合計を求めます。
偏差平方和についてはこちらでも紹介しています
よろしかったらどうぞ
分散
分散とは、
データのバラツキ具合の平均
です
計算式のように書くと、
分散 = データのバラツキ具合の合計 / データ数
ということです。
データのバラツキ具合の合計とは、「偏差平方和」のことです。
分散は、その合計をデータ数で割ったものです。
つまり、平均ですね。
散らばりの平均が出せるため、
- 分散が大きいほど、各データがバラけている
- 分散が小さいほど、各データがバラけておらず、平均付近のデータが多い
ことがわかります。
求め方は、
です。
この \(\sigma ^{2}\)が分散です。
その偏差平方和をデータの数nで割ったのみです。
分散についてはこちらでも紹介しています
よろしかったらどうぞ
標準偏差
標準偏差とは、
データのバラツキ具合の平均
です。
あれ?読んだことあるな?と思った人もいるのではないでしょうか。
そうです。
こちらは、分散と同じ説明です。
実は分散は値の大きさからの比較がしづらいです。
なぜなら、標準偏差を出す時に距離を2乗してしまっているからです。
確かに、分散はバラツキの具合の平均として比べる指標です。
しかし、2乗してしまっているため、分散で出た値は
実際のバラツキ具合の平均の2乗
になります。
そのため、分散は非常に大きな値になることがあります。
そして、その数値が距離の平均ではありません。
そのため、√ (ルート) を使用して、2乗を消しましょう。
求め方は
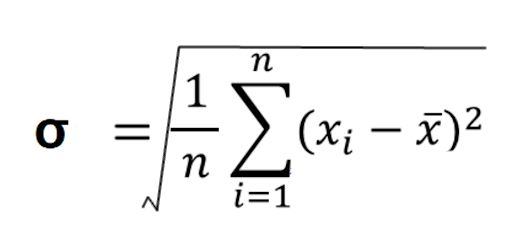
です。
これにより、実際のバラツキ具合の平均が求められます。
- 標準偏差が大きければ、そのデータ集団は平均からバラツキがある
- 標準偏差が小さければ、そのデータ集団は平均からバラツキがあまりない
ということがわかります。
標準偏差についてはこちらでも紹介しています
よろしかったらどうぞ
偏差値
偏差値とは、
平均からのデータの優秀さ
を表します。
求め方は、
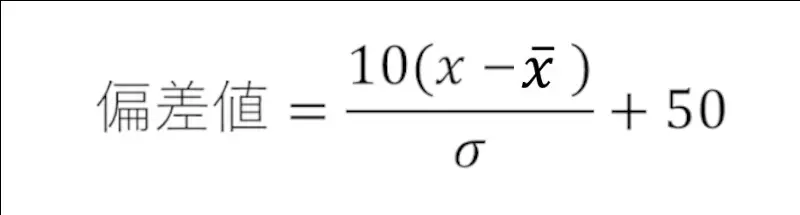
です。
先程、標準偏差を求めました。
そして、偏差値は平均値を
50
とします。
そして、平均値から
- 標準偏差1つ分足した値を60
- 標準偏差2つ分足した値を70
- 標準偏差1つ分減らした値を40
- 標準偏差2つ分減らした値を30
とします。
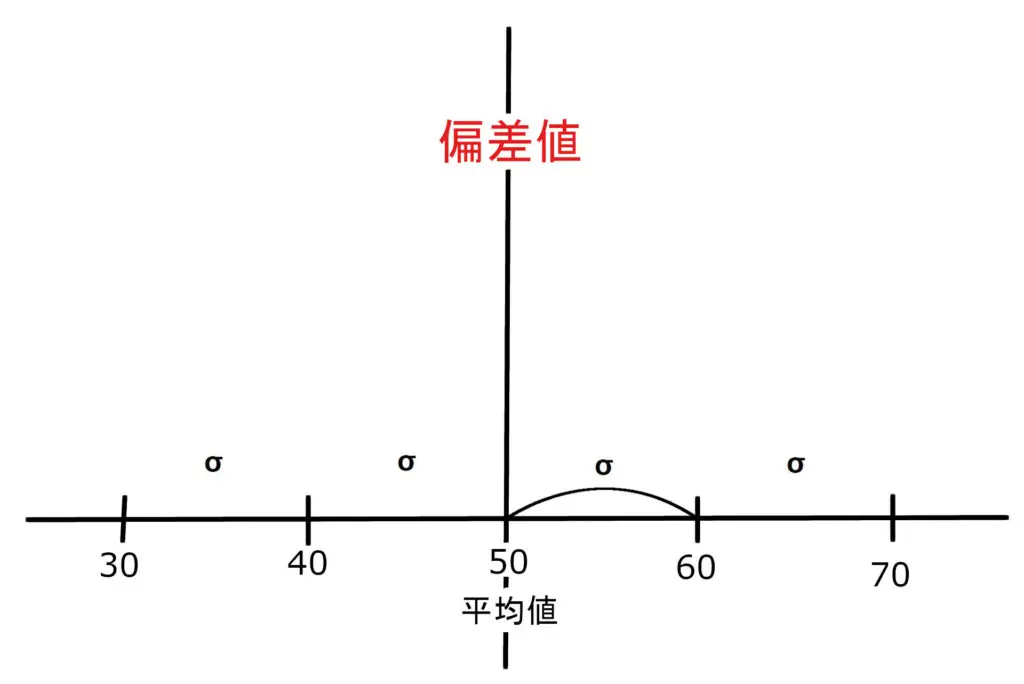
そして、データの量が増えていくと、各データの割合は、
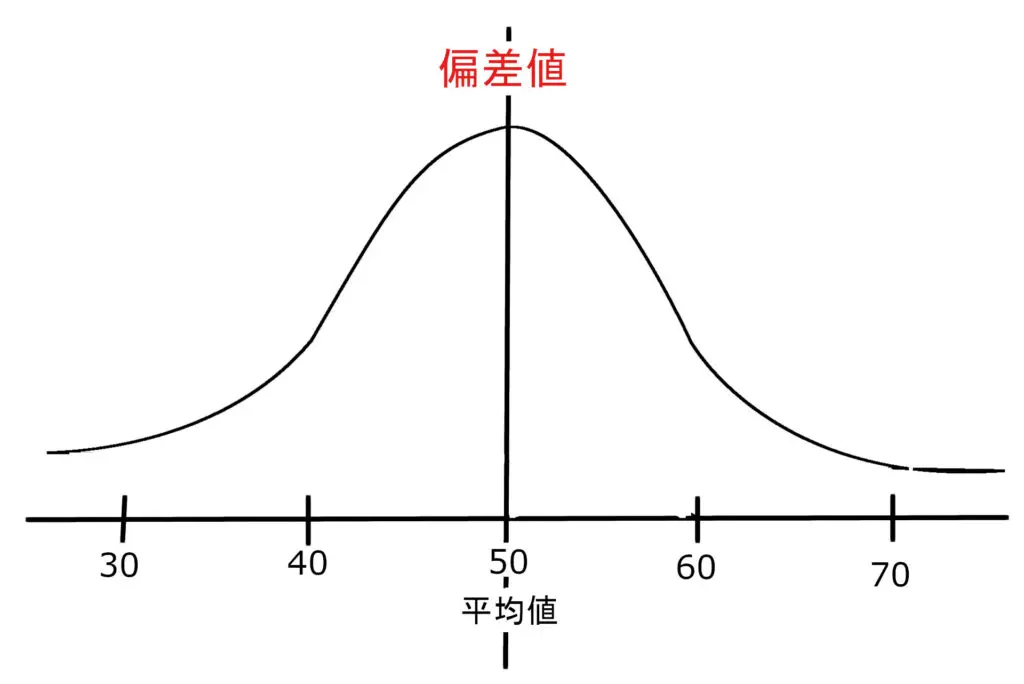
のようになります。
つまり、偏差値50のデータがより多く、
離れるにつれて割合が少なくなっていくということです。
よって、各データの偏差値が、
- 60なら優秀
- 70なら非常に優秀
- 40ならあまり良くない
- 30なら危険
という判断基準ができます。
しかし、データ量が少ないとこのようなグラフにならないので、
偏差値で判断する場合、ある程度の量のデータが必要です。
偏差値についてはこちらでも紹介しています
よろしかったらどうぞ
まとめ
今回は、
バラツキから集団を比較するときの指標
について紹介させていただきました。
指標には、
「偏差」「偏差平方和」「分散」「標準偏差」「偏差値」
などがあります。
実際に、よく比較に使用する指標は、
標準偏差・偏差値
です。
他の指標も使うことがありますが、主に2つの値を求めるために使用します。
標準偏差を求めるために、
平均値 → 偏差 → 偏差平方和 → 分散 → 標準偏差
と順番に求めて行きましょう。
平均値からいきなり標準偏差を求めようとすると、なかなか難しく感じます。
一つづつ何を求めているかを理解できれば、
難しいことはしていないので、一つづつ理解して行きましょう。
最後まで読んでいただき、ありがとうございました。
コメント