変動係数 = 標準偏差 ÷ 平均値
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
変動係数
について勉強していこうと思います。
変動係数
変動係数とはバラツキを比べやすくするもの
変動係数とは、
単位をなくしてバラツキを表す係数
です。
バラツキが大きいほど変動係数も上昇し、小さいほど変動係数も下降します。

単位をなくして比べることができるため、
単位の違うデータのバラツキを比較することができます。
用途
変動係数は、
平均値の異なるデータや単位の異なるデータを標準偏差 (平均からのバラツキ) で比較する
時に使用します。
理由は平均値や単位が違うとバラツキのみでは比較しくいから
複数の値を比較するとき、
平均値だけでなく標準偏差 (平均からのバラツキ) からも比較する
ことで気づけることがあります。

こちらの集合の方がバラツキが小さいから
今後データも平均値付近になりやすいだろう
などの推測ができます。
しかし、平均値や単位の違う二つのデータをバラツキの値のみで比較することができるでしょうか?
”平均売上1万円 標準偏差6000円のお店A”と“平均売上4万円 標準偏差2万円のお店B”の場合
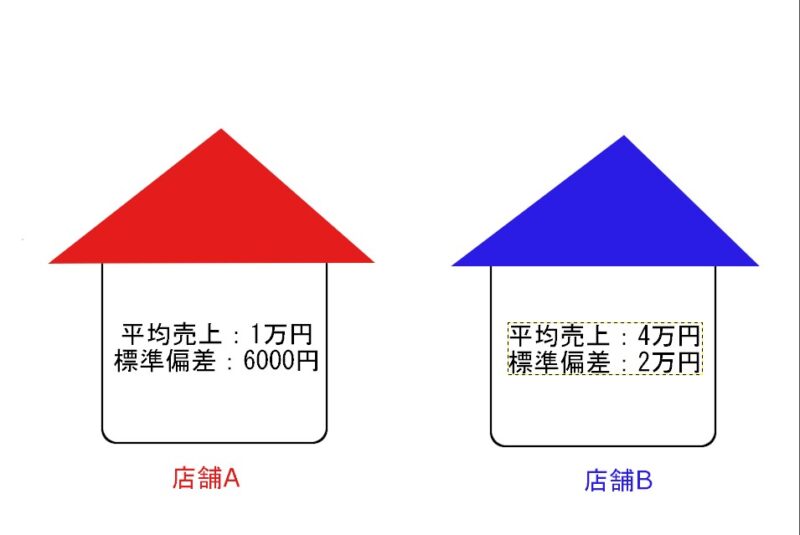
標準偏差のみで比べると、
Aは6000円:Bは2万円
です。
標準偏差のみで比較すると、

値の大きい方がバラツキは大きいので、Bの方がバラツキ具合は強い
となります。
しかし、本当にそうでしょうか?
求め方は標準偏差を平均値で割るだけ
変動係数の解き方は、
変動係数 = 標準偏差 ÷ 平均値
です。
例
平均値の違うデータの場合
先程のお店Aとお店Bを変動係数を使用して比較してみましょう。
A:平均売上1万円・標準偏差6000円
B:平均売上4万円・標準偏差2万円


標準偏差のみで比較するとBの方が大きいためバラツキ具合はBが強いと考えられますよね。
では、変動係数で比較するとどうでしょうか?
1、変動係数を求める
変動係数は、
変動係数 = 標準偏差 ÷ 平均値
です。
A:6000円 ÷ 1万円 = 0.6
B:2万円 ÷ 4万円 = 0.5
2、比較する
Aの変動係数は0.6
Bの変動係数は0.5
変動係数はAの方が大きいです。
つまり、
Aの方が平均値に対するバラツキは大きい
ということです。
単位が違うデータの場合
変動係数は単位をなくすことができるため単位が違うデータの比較にも使用できます。
お店A:平均売上1万円・標準偏差6000円
Bさんの労働時間:平均5時間・標準偏差1時間
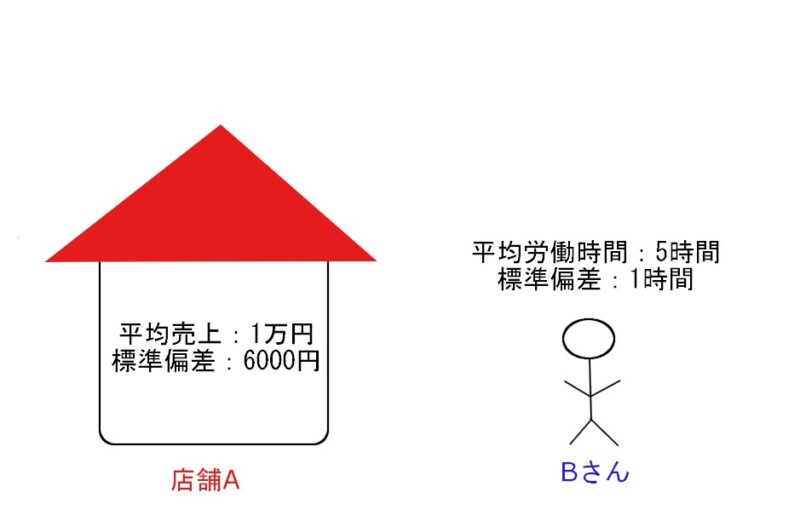

このままでは比べようないですね。
1、変動係数を求める
変動係数は、
変動係数 = 標準偏差 ÷ 平均値
です。
A:6000円 ÷ 1万円 = 0.6
B:1時間 ÷ 5時間 = 0.2
2、比較する
Aの変動係数は0.6
Bの変動係数は0.2
変動係数はAの方が大きいです。
つまり、
Aの方が平均値に対するバラツキは大きい
ということです。

このように単位の違う二つのデータを比較する時にも使えます。
まとめ
今回は、
変動係数
について紹介させていただきました。
変動係数は、
標準偏差 (バラツキ) を比べやすくするもの
です。
複数のデータを標準偏差で比較するとき、
- 平均値が違う
- 単位が違う
場合、そのまま標準偏差の値で比較するのは難しいです。
その時に、平均値と標準偏差を使用して変動係数を求めることで、二つのデータを比べることができるようになります。
求め方は、
変動係数 = 標準偏差 ÷ 平均値
です。
最後まで読んでいただき、ありがとうございました。



コメント