標準偏差±1に約68%・±2に約95%
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
偏差値
について勉強していこうと思います。
たくさんのデータから傾向を調べるときに使用するものの一つに平均値があります。
しかし、
- 平均値が同じだから同じような傾向のデータ
- 平均値が全然違うから全く傾向が違うデータ
とは言い切れません。
そんなときに使用する指標の一つが偏差値です。
それではよろしくお願いします。
偏差値
偏差値とは
偏差値とは、
一つのデータが平均値から見てどのくらいの位置にいるかを知る指標
です。

学生の時にテストの結果でよくでましたね。
偏差値では、まず平均値が偏差値50になります。

つまり、
偏差値50のデータ=平均値
というわけですね。
偏差値は、この50を基準に考えます。
この平均値から標準偏差1つ分プラスした箇所を偏差値60、2つ分プラスした箇所を偏差値70とします。
逆に、平均値から標準偏差1つ分マイナスした箇所を偏差値40、2つ分マイナスした箇所を偏差値30とします。
グラフで表すと、
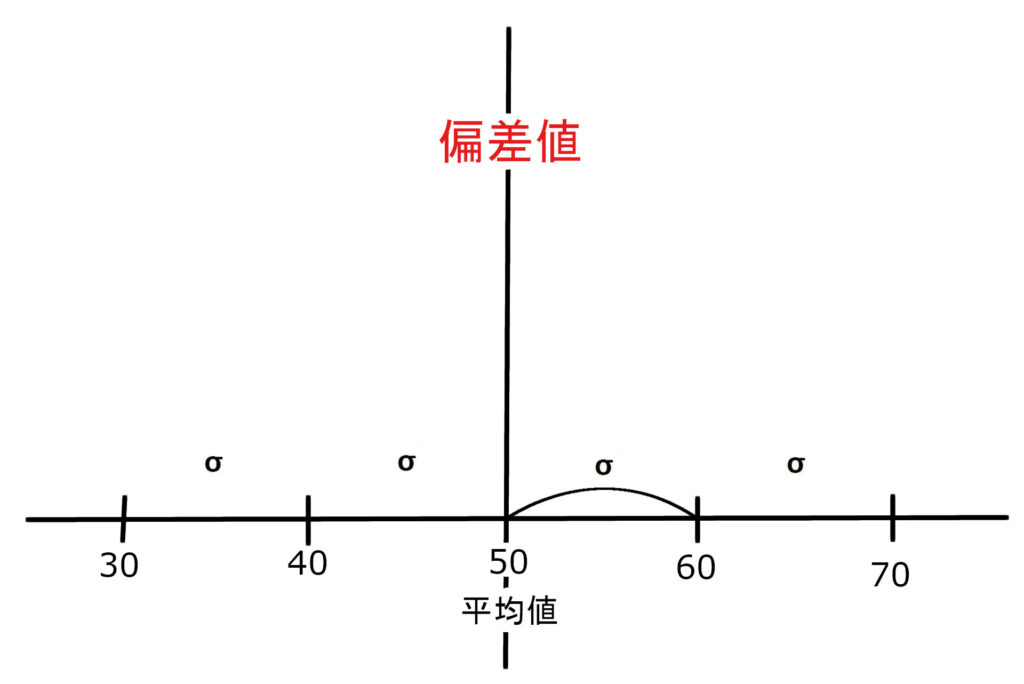
このようになります。
また、そのデータ群が正規分布に近いなら、
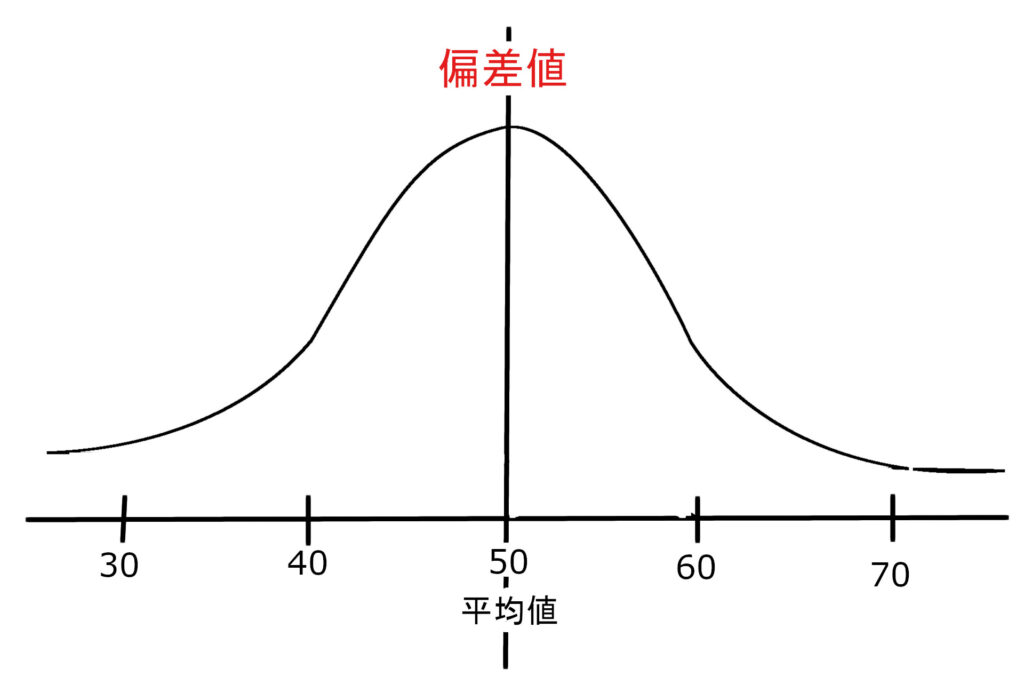
ヒストグラムはこのようになります。
そして、
偏差値40~60の間に約68%・偏差値30~70の間に約95%
のデータがが入ります。

つまり、偏差値30より小さい、または偏差値70より大きいデータは、全体の約5%しかないということです。
求め方
求め方は、
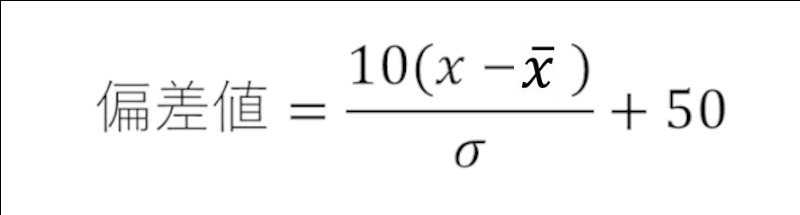
です。
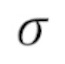 が標準偏差・
が標準偏差・ がそのデータ・
がそのデータ・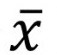 がデータの平均値
がデータの平均値
用途
偏差値を求めることにより、
「そのデータが全体のどの位置にいるのか」「これからのデータがどの範囲内に出る可能性が高いか」
を知ることができます。
そのデータが全体のどの位置にいるのか
先程のグラフを見てわかる通り、正規分布に近いデータ群は偏差値40~60の間にデータが集まります。

偏差値40~60までのデータが多いということです。
つまり、
偏差値60以上なら優秀・偏差値40以下ならあまり良い位置にいない
と考えられます。
これからのデータがどの範囲内に出る可能性が高いのか
偏差値というのは、
40~60の間に約68%・30~70の間に約95%
のデータが入ります。
つまり、これから同じ条件で新しいデータを取っていくときも、その間になる可能性が高いという予測が立てられます。

ほぼ30~70の間に入り、40~60の間になる可能性が高いということです。
特徴
平均値などの違いではみられない違いがわかることもある
分散などと同じように、平均値・中央値・最頻値がどれも同じでも、全く違うヒストグラムになる事がよくあります。
平均からのバラツキから違いを考えてみましょう。
データの傾向が掴みやすくなる
偏差値を求めることで、
以降のデータがどの範囲内になる可能性が高いか
が予測できます。
- 偏差値40~60の間になる可能性が約65%
- 偏差値30~70の間になる可能性が約95%
という予測が立てられます。
しかし、あくまで統計であり予測です。
その範囲以外の値が出る可能性が約5%あります。
また、データが増えるうちに標準偏差も変化していくこともあります。
しかし、かなりのデータで計算した場合は大きく変化はなくなります。

途中の計算でデータ数が分母のため、一つの値が与える影響が少ないですからね。
例
データから予測してみよう

1、度数分布表とヒストクラムの作成

ヒストグラムにすると、
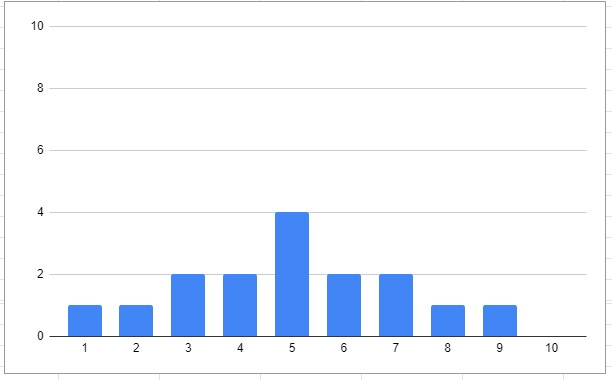
です。
2、「データの数」・「値の合計」を算出
データの数は
1 + 1 + 2 + 2 + 4 + 2 + 2 +1 + 1 = 16
です。
値の合計は
1×1 + 2×1 + 3×2 + 4×2 + 5×4 + 6×2 + 7×2 + 8×1 + 9×1
= 1 + 2 + 6 + 8 + 20 + 12 + 14 + 8 + 9 = 80
です。
3、「平均値」を算出
平均値は、値の合計 / データの数 のため、
80 / 16 = 5
です。

この値が偏差値50になります。
4、「偏差」を算出
偏差は、各データの平均との差のため、
1 – 5 = –4が1件
2 – 5 = -3が1件
3 – 5 = -2が2件
4 – 5 = -1が2件
5 – 5 = 0が4件
6 – 5 = 1が2件
7 – 5 = 2が2件
8 – 5 = 3が1件
9 – 5 = 4が1件
です。
5、「偏差平方和」を算出
偏差平方和は、各偏差の2乗の合計のため、
{ (-4)2 × 1 } + { (-3)2 × 1 } + { (-2)2 × 2 } + { (-1)2 × 2 } + { 02 × 4 } + { 12 × 2 } + { 22 × 2 } + { 32 × 1 } + { 42 × 1 }
= 16 + 9 + 8 + 2 + 0 + 2 + 8 + 9 + 16
= 70
です。
6、「分散」を算出
分散は、偏差平方和 / データの数のため、
70 / 16 = 4.375
です。
7、「標準偏差」を算出
標準偏差は、√分散のため、
√4.375 ≒ 2.09
です。
つまり、こちらのデータは、平均値から平均で2.09上下にバラけているということになります。
8、ヒストグラムに標準偏差を入れる
平均値5・標準偏差2.09なので、
- 偏差値60は5 + 2.09 = 7.09
- 偏差値70は 5 + 2.09 × 2 = 9.18
- 偏差値40は、5 – 2.09 = 2.91
- 偏差値30は、5 – 2.09 × 2 = 0.82
となります。
これをグラフに入れると、

このようになります。
この結果、
2.91 ~ 7.09 に約65%・0.82 ~ 9.18 に約95%
入ると予測が立てられます。
今回のデータは一桁の数字で計算したためわかりにくいかもしれません。
全てのデータを1万円かけてお店の売り上げで考えてみましょう。
| お店 | |
| 日数 | 16日 |
| 総売上 | 80万円 |
| 平均値 | 5万円 |
| 偏差平方和 | 70万 |
| 分散 | 4.375万 |
| 標準偏差 | 2.09万円 |
このようになります。

「偏差平方和」「分散」は2乗した値だということを忘れないようにしましょう。
平均売り上げは5万円・標準偏差は2.09万円です。
つまり、偏差値50は5万円になります。
また、
- 偏差値60は、5万円 + 2.09万円 = 7.09万円
- 偏差値70は、5万円 + 2.09万円 × 2 = 9.18万円
- 偏差値40は、5万円 – 2.09万円 = 2.91万円
- 偏差値30は、5万円 – 2.09万円 × 2 = 0.82万円
となります。
これにより、
「売上7.09万円より上は優秀」「2.91万円より下はあまり良くない」
と考えられます。
そしてこれからの売上は、
2.91万円 ~ 7.09万円の間に約65%・0.82万円 ~ 9.18万円に約95%
が入ると予測できます。
注意点
ある程度のデータ数が必要
データが少ないと、増えるごとに平均値・標準偏差が大きく動く可能性があります。
ここまでの説明の通り、偏差値は平均値と標準偏差により比較ができます。

つまり、一つのすごく大きなデータ一つで一気に平均値・標準偏差が変わってしまうことがあるということです。
平均値・標準偏差が変われば、偏差値も変わってしまいます。
そのため、あまり正確な予測は立てられません。
なので、予測は立てられますがデータ数が多いほど正確な予測が立てられるので、ある程度のデータを集めましょう。
まとめ
今回は、偏差値について紹介させていただきました。
この値から、一つ一つのデータの優秀さを求めることができます。
平均値を偏差値50として、
- 平均値 + 標準偏差 = 偏差値60
- 平均値 – 標準偏差 = 偏差値40
のように値を求めて、そのデータがどの位置に値するかを見ましょう。
また、偏差値を求めることにより、これからのデータ予測も立てられます。
偏差値40~60に約65%・偏差値30~70に約95%
です。
注意点として、
あまりデータの数が多くないと平均点・標準偏差が大きく動く可能性がある
ため、ある程度のデータ数が必要です。
最後まで読んでいただきありがとうございました。



コメント