3つの中央値
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
四分位数
についてです。
箱ひげ図を書くときに使われる数値は、
最小値・第一四分位数・中央値・第三四分位数・最大値
の5つです。

最小値・中央値・最大値は聞いたことあるのではないでしょうか?
この中で、
第一四分位数・第三四分位数
という値があります。

この2つの値は、言葉のままではどのような値かわかりにくいですよね。
この記事を読めば、
箱ひげ図がなぜ、25%ずつに分かれるのか
が理解できます。

箱ひげ図を使用するとき、必ず使う値です。
一緒に学びましょう。
四分位数
四分位数とは
四分位数とは、
データの数を4等分した時のそれぞれの値
です。
四分位数のため、4等分した値
m分位数なら、m等分した値になります。

つまり、五分位数なら、5等分したそれぞれの値ということですね。
4つにグループ分けした内の
- データ数の1/4番目を第1四分位数
- データ数の2/4番目を第2四分位数
- データ数の3/4番目を第3四分位数
- データ数の4/4番目を・・・
この流れでいくと、4/4番目を第4四分位数と言いそうですね。
しかし、そうは言いません。
なぜなら、4/4番目の値は、
最大値
だからです。
そのため、第4四分位数を言わずに最大値と言いましょう。

ちなみに、2/4番目の値は、
中央値
になります。
なので、第2四分位数ではなく、中央値と呼ぶ方が多いですね。
第1四分位数・第3四分位数
ここまでで、四分位数がどの値になるかを学びました。
第2四分位数とは、
全体の中央値
でしたね。
では、第1四分位数と第3四分位数はなにになるでしょうか?
第1四分位数
最小値から中央値までの中央値
第3四分位数
中央値から最大値までの中央値
と考えることができます。
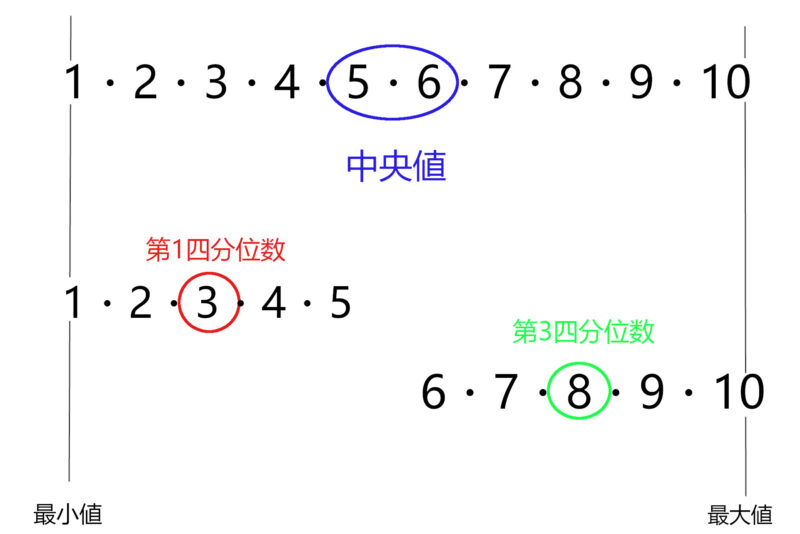
つまり、第1四分位数・第2四分位数・第3四分位数を求めるということは、
3つの中央値を求める
ということです。
用途
四分位数は、主に
- 真ん中50%の範囲を求める
- 箱ひげ図の作成
に使用します。
真ん中50%の範囲を求める
第1四分位数・中央値・第3四分位数は、
3つの中央値
です。
そのためデータ数では、
- 最小値から第1四分位数で25%
- 第1四分位数から中央値で25%
- 中央値から第3四分位数で25%
- 第3四分位数から最大値で25%
になります。
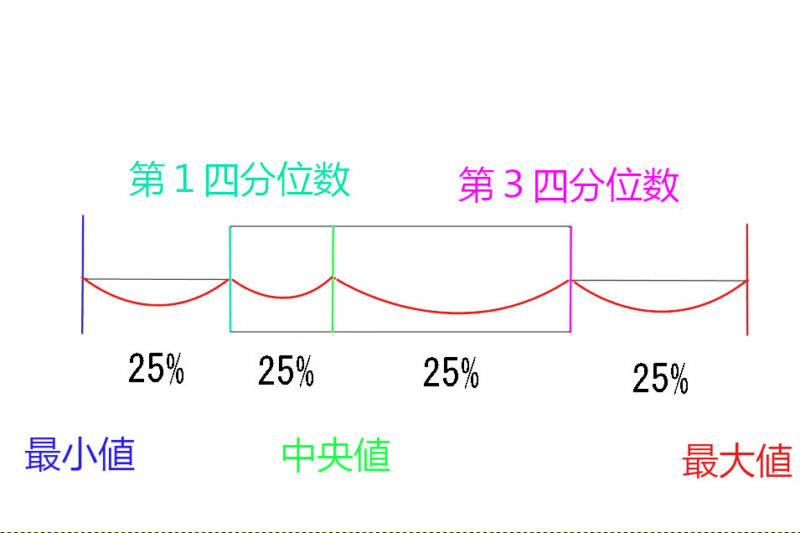
つまり、
第1四分位数から第3四分位数までで50%のデータ数がある
ということです。
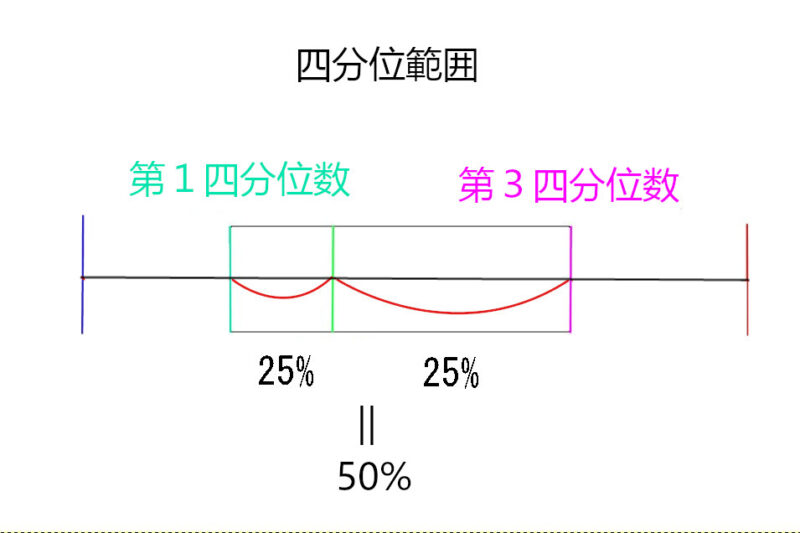

この範囲を四分位範囲と言います。
箱ひげ図の作成
平均値はたった一つの極端な値に大きく影響されます。
そのため、平均値のみで統計を見るのは危険です。
その中、箱ひげ図は平均値を全く使わない図になるため、極端な値の影響はありません。
その箱ひげ図には、
- 第1四分位数
- 第2四分位数 (中央値)
- 第3四分位数
3つとも使用します。
箱ひげ図に関しては、こちらでも紹介しています
よろしかったらどうぞ
求め方
小さい順に並べる → 中央値 → 第1四分位数・第3四分位数
1、小さい順に並べる
中央値を求めるため、
値を順番に並べる
必要があります。
2、中央値を求める
四分位数を求める時まず先に、
中央値
を求めます。
中央値は、データを順番に並べた時の、真ん中の値です。
中央値はこちらで紹介しています
よろしかったらどうぞ
3、第1四分位数・第3四分位数を求める
中央値を求めたため、
最小値から中央値の中央値:第1四分位数
中央値から最大値の中央値:第3四分位数
と求めましょう。

こちらも範囲が変わっただけで、
求めるのは中央値です。
例
3・5・7・6・7・1・3・4・10・1
1、小さい順に並べる
小さい順に並べましょう。
1・1・3・3・4・5・6・7・7・10
2、中央値を求める
並べた値から、中央値を求めます。
データ数が10ですので、
5番目と6番目の真ん中
です。

ここでは、4と5ですね。
( 4 + 5 ) / 2 = 4.5
3、第1四分位数を求める
第1四分位数のため、
最小値と中央値の中央値
です。

今回、中央値は4.5でしたが、値の中では4になります。
よって、
1・1・3・3・4
から中央値を求めます。
真ん中なので3です。
第1四分位数は3です
4、第3四分位数を求める
第3四分位数のため、
中央値と最大値の中央値
です。

今回、中央値は4.5でしたが、値の中では5になります。
よって、
5・6・7・7・10
から中央値を求めます。
真ん中なので、7です。
第3四分位数は7です
まとめ
今回は、
四分位数
について紹介させていただきました。
四分位数とは、
データを四等分した時のそれぞれの値
です。
第2四分位数は中央値です。
また、
- 第1四分位数は最小値から中央値までの中央値
- 第3四分位数は中央値から最大値までの中央値
です。
そのため、第一四分位数・中央値・第3四分位数で
3つの中央値
になります。
用途としては、
- 真ん中の50%の範囲を求められる
- 箱ひげ図に使用する
時に使用します。
最後まで読んでいただきありがとうございました。




コメント