他のデータを使って式や値で説明すること
こんにちは、徳です。
デジタルDIYができるようコーディング・プログラミング・画像加工・動画編集などを本やYouTubeで勉強しています。
現在は、初心者なので、とにかくゆっくり進んでいくと思います。
また、「間違っていること」や「こうした方が良いよ」などがあれば、コメントなどしていただけたら幸いです。
では、いきましょう!
統計学
今回は、
回帰
についてです。
2つのデータ群の関係を求めるとき、どんな値を求めて調べるか覚えていますか?
答えは、
相関係数
です。

相関係数によって、データ間の相関関係を知ることができましたね。
ここで、

相関関係はわかったけれども、実際に数値としてどのくらい増える関係かを知りたい。
と思ったことないですか?
その時に使用するものが、回帰です。
回帰を使えば、
項目間の関係を読み解く
ことができるようになります。
回帰
回帰とは
説明
回帰とは、
お互いの項目間の関係を読み解く
ことです。
つまり、
データを他のデータを使って式や値で説明する
ということです。

片方が1増えたら、もう片方は〇〇増える関係にある
などの式や数値で説明できたら、これからの予測にも役立ちますよね。
用途
回帰は、
データの予測
に使用します。

これを、回帰分析と言います。
回帰を考えることで、
データ間を式で表すことができる
ようになります。

y = ax + bのような式を作ります。
これを、回帰直線と言います。
関係を式で表すことにより、
片方の値が〇〇ならもう片方は××になる
と考えることができるようになります。
相関との違い
2つのデータの関係を表すものとして、
相関係数などを使用した相関関係
というものがあります。
回帰と相関関係の違いは、
相関関係
お互いの関係を強さと向きで表す
xが増えればyも増えるなど
回帰
お互いの関係を式などで表す
xが決まればyも決まる
という点です。
しかし、回帰直線を求める場合、
その前に相関関係があるかを確認する
ことが多いです。

無相関の場合、直線で表すことは難しいですからね。
回帰の流れ
回帰の流れは、
相関があるかを調べる
↓
回帰直線を引く ( y = ax + b の式にする)
↓
回帰直線の係数a・bを求める
↓
y = ax + bに代入 (式が完成します)
↓
残差を求める
↓
残差平方和を求める
↓
決定係数を求める
↓
決定係数で比較する
です。
使われる言葉
回帰を考えるときによく使われる言葉として、
回帰直線・残差・残差平方和・決定係数
というものがあります。
実際に、比較する時に使われるのは、
回帰直線と決定係数
です。
回帰直線を求めることで、2つのデータの関係を
y = ax + b
の形にできます。

式にすることで、
xのデータを仮定したときのyを予測する
ことができるのです。
また、決定係数を求めることで、決定係数が
0に近いほど
xがyを説明できていない
1に近いほど
xがyを十分説明できている
と言えます。
残差と残差平方和は、
決定係数を求めるため
に求めます。
回帰
ここからは、回帰の流れを簡単に見ていきましょう。
2つのデータの関係を式にする
相関があるかを調べる
まずは2つのデータの相関があるかを調べましょう。
相関があるかを調べるには、
散布図・相関係数
を使用します。
相関の調べ方は、こちらで紹介しています
よろしかったらどうぞ
この時に、
無相関であった場合、回帰直線を求めるのは難しい
です。
無相関ということは、
2つのデータに関わ理がない可能性が高い
ということだからです。

関わりがなければ、式にすることができませんよね。
関係を式にすることが回帰なので、
できないのなら、ここでやめましょう。
回帰直線を引く
相関を調べて、相関があったらしきにするため
回帰直線を引く
ようにしましょう。

ここでは、特に行うことはありません。
y = ax + bの式を考えよう
ということです。
回帰直線の係数a・bを求める
y = ax + bの式を完成させるため、
係数a・b
を求めましょう。
y = ax + bに代入
先ほど求めた、係数a・bを、
y = ax + b に代入
しましょう。

求めたaとbを入れるだけですね。
これで、
2つのデータの関係を式にする
ことができました。

回帰の目的の一つ「関係を式にする」が、
これでできましたね。
決定係数を求める
ここからは、決定係数を求めましょう。
残差を求める
まずは、残差を求めます。
残差とは、
式にしたときの各データと実際のデータとの差
です。
先ほど作成した式は、
データから作った一番近い式
です。
近い式であるため、
実際に集めたデータと、式にxを代入したときのyの値は常に同じとはならない
と言うことです。
残差とは、その時の
実際のデータと代入した時の値の差
です。
残差平方和を求める
残差を求めたら、残差平方和を求めましょう。
残差平方和とは、
残差
式の値と実際の値の差
平方
2乗
和
合計
です。
つまり、
式の値と実際の値の差を2乗した合計
と言うことです。

公式もそのままですね。
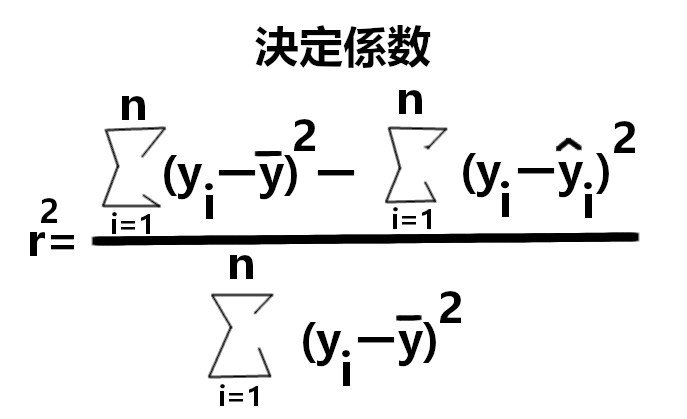
決定係数を求める
決定係数とは、
実際のデータがどのくらい回帰直線に沿っているのか
を表します。

この値を求めることで、
式がどのくらい近い値を説明しているのか
を知ることができます。
これで、決定係数を求められました。
決定係数で比較する
決定係数を求めたら、
その値で比較
をしましょう。
比較の仕方の例としては、
- 0.6以下:説明できていない
- 0.65 より大きく0.8付近:よく説明できている
- 0.9以上:大きすぎる・あまりにも合っているため、予測としては不安と考える
です。

人によって、見方は変わります。
しかし、0.9以上はあまりにも高すぎる
と考えた方が良いと私は思います。
注意点
「決定係数が高い = 関係がある」ではない
決定係数は、
あくまで今までのデータが式の近くの値に沿っている
というのみの値です。
つまり、
決定係数が高い = 2つのデータには関係があると言うわけではない
ということです。
まとめ
今回は、
回帰
について紹介させていただきました。
回帰とは、
データを他のデータで説明する
と言うことです。
回帰をする目的は、
- 2つのデータを式で説明する
- 式がデータにどのくらい沿っているのかを見る
です。
最後まで読んでいただき、ありがとうございました。


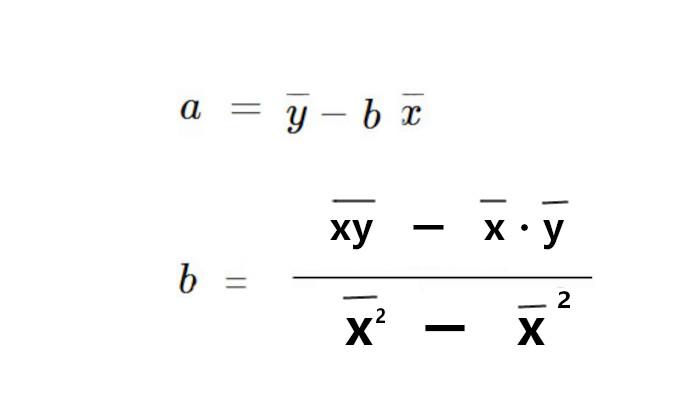
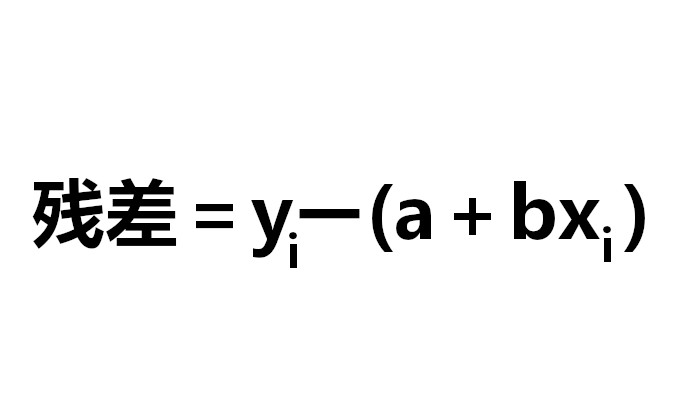
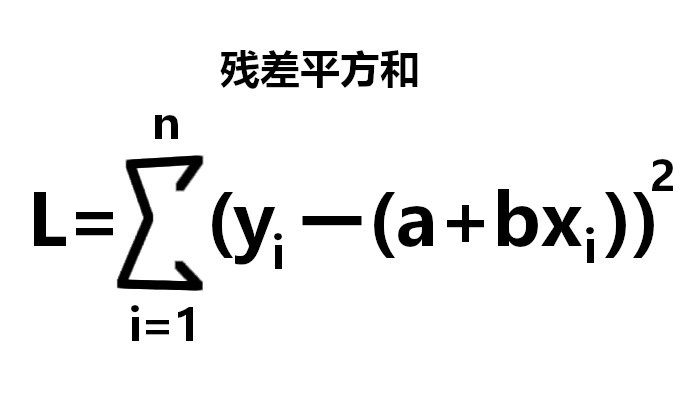


コメント